Тесты по геометрии 9 класс. Тема: "Уравнение окружности"
Правильный вариант ответа отмечен знаком +
1. Задана точка O с координатами a и b. Также имеется центр окружности A с координатами c и d. Среди приведенных выражений нужно выбрать верное для нахождения величины расстояния от точки, лежащей на окружности, до центра этой окружности.
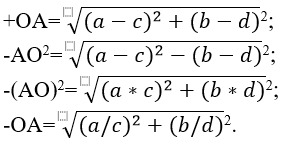
2. Даны две точки окружности. Одна является его центром, другая принадлежит окружности. Каким образом правильно записать их координаты?
-T (F; H), J (D; P);
-G=h; g;
-DF(bv; nk);
+O (f; d), F (g; r).
3. Имеется центр окружности A (4; 2) и точка, находящаяся на окружности R (5; 3). Расстояние от центра окружности до данной точки будет находиться следующим образом:
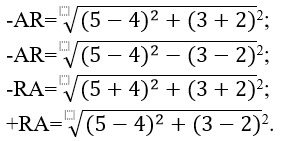
4. Которое из имеющихся выражений не является уравнением окружности или содержит ошибку?
![]()
-r2= (f – d)2 + (g – h)2;
+EW= а+с;
-x2= d2 + h2.
5. Уравнение окружности с центром в начале координат никогда не примет вид:
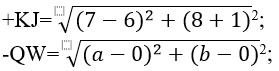
- r2=t2 + e2;
- v2= (f – 0)2 + (g – 0)2.
6. При выведении уравнения окружности нужно задать?
- трёхмерная система координат;
- четырёхмерное пространство;
- ничего не задаётся;
+ прямоугольная система координат.
7. Задана окружность с центром в определённой точке. Она проходит через начало координат. Можно ли вычислить радиус этой окружности?
+ да;
- нельзя;
- лишь частично;
- нужно делать дополнительные построения.
8. Существует окружность с точкой F (8;6). Это её центр. Окружность проходит через начало координат. Каков радиус этой окружности?
- 15;
- 14;
-4;
+ 10.
9. Точка X (4; 3) является центром окружности. Окружность же проходит сквозь начало координат. Верное уравнение окружности для данной задачи.
+(x-4)2+(y-3)2=25;
-(4-x)2+(3-y)2=25;
-25= (x+4)2+(y-3)2;
-25= (x+4)2+(y+3)2.
тест 10. Точка D с координатами (7; 6) – центр заданной окружности. Она является проходящей через начало координат. Уравнение окружности будет иметь вид:
-x2+16x+y2-12y+82=85;
-85=x2+14x+y2+14y+83;
+85=x2-14x+y2-12y+85;
-2x2-16x-y2-12y+85=85.
11. Среди рисунков выбрать тот, что иллюстрирует окружность, заданную уравнением 3 = x2+y2.

12. Задано уравнение окружности 132= x2-18x+y2+16y+149. Принадлежит ли этой окружности точка T(1; 0)?
- не принадлежит;
- без построения рисунка сказать невозможно;
- всё зависит от обстоятельств;
+ принадлежит.
13. Как возможно узнать принадлежит ли точка данной окружности?
+ нужно найти расстояние от точки до центра окружности и, если данное расстояние будет равно радиусу, точка принадлежит окружности;
- потребуется подставить координаты точки в уравнение окружности и, если полученное значение не будет равно радиусу, точка лежит на окружности;
- нужно узнать равно ли расстояние от точки до центра окружности, если равно, значит такая точка лежит внутри данной окружности;
- следует узнать величину от точки до центра окружности и сравнить с радиусом, если эта величина будет меньше радиуса, значит точка лежит на окружности.
14. Если величина расстояния от точки до центра окружности будет больше радиуса этой окружности, то данная точка лежит…
+ вне окружности;
- на данной окружности;
- внутри окружности;
- нельзя сказать.
15. Расстояние от центральной точки окружности меньше радиуса окружности. Это значит только то, что …
- точка находится вне окружности;
- точка располагается на окружности;
+ точка лежит внутри окружности;
- без построения окружности ничего сказать нельзя.
16. Нужно выяснить принадлежит ли точка W (7; -9) окружности с уравнением 16= (x-7)2+(y+5)2. Требуется указать самый подходящий ответ.
+ принадлежит, так как 16= (7-7)2+(-9+5)2;
- не принадлежит, потому, что 16≠ (0)2+(-2)2;
- точка лежит на окружности, ведь 16≠ (7+7)2+(-9)2;
- нельзя точно сказать из-за того, что 16= 02+52.
17. Нужно указать принадлежность точки окружности, если дано уравнение 10= (x-7)2+(y+5)2 и точка Q (8; -8).
- эта точка не принадлежит ни одной окружности;
+ точка имеет принадлежность к окружности 10= (x-7)2+(y+5)2;
- 10= (8-7)2+(-8+5)2 – к данной окружности точка Q (8; -8) не имеет никакого отношения;
- сложно сказать без рисунка.
18. Есть уравнение окружности 2x2- 8x+2y2+6y+149=132 и точка K (3; 2). Требуется указать степень принадлежности её к окружности.
- данная точка будет принадлежать окружности;
- точка лежит внутри окружности;
+ точка находится вне окружности;
- без чертежа этого не скажешь.
19. Имеется точка S с координатами (x; y). Какая из координат называется абсциссой?
+ x;
- y;
- нет верного ответа;
- обе координаты.
тест-20. Есть точка J (x; y). Координата, называемая ординатой это…
- здесь нет верного ответа;
- обе из координат;
-x;
+y.
21. Есть уравнение окружности 16= (x-6)2+(y+9)2. Найти точку, принадлежащую окружности, с абсциссой 10.
+G (10; -9);
-H (10; 5);
-K (8; 0);
-F(4; -5).
22. Имеется уравнение окружности 64 = (x-15)2+(y+14)2. Найти точку, имеющую принадлежность окружности, с ординатой - 6.
-Z (11; -6);
-V (6; -6);
-M (-6; 5);
+C (0; -6).
23. Среди рисунков выбрать тот, который содержит точку S (5; 1), принадлежащую окружности с уравнением 5 = (x-4)2+(y+1)2.
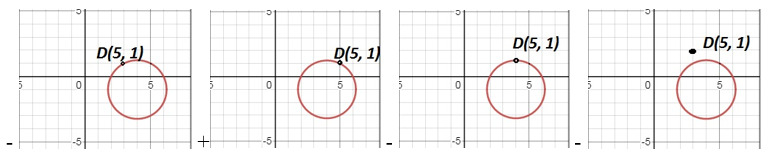
24. Линия, соединяющая пару точек, лежащих на окружности, будет называться:
- медиана;
- биссектриса;
- радиус;
+ хорда.
25. Отрезок, выходящий из центра окружности, соединяющийся с любой её точкой, принято называть:
- медианой;
+ радиусом;
- биссектрисой;
- хордой.
26. Проверить принадлежность точек F (1; 1) и H (-7; -7) к окружности с уравнением 32=(x+3)2 + (y+3)2.
- обе не принадлежат;
- принадлежит только F (1; 1);
- лежит на окружности лишь H (-7; -7);
+ обе принадлежат.
27. Даны точки H (-8; -8), F (2; 2) и уравнение некоторой окружности вида 32=(x-3)2 + (y-5)2. Будет ли через эти точки проходить хорда окружности?
- будет;
+ нет;
- нужно строить чертёж;
- нет верного ответа.
28. Выбрать окружность, проходящую через начало координат.
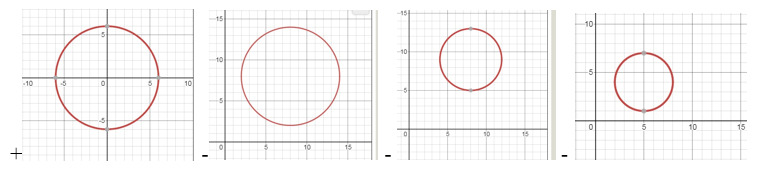
29. На каком из рисунков изображена хорда окружности?
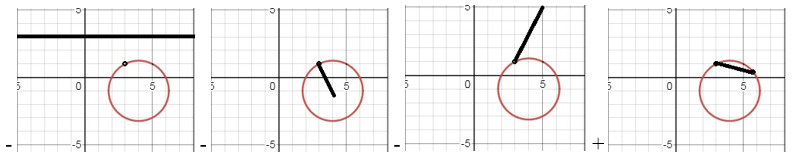
тест_30. Можно ли вычислить радиус окружности, если известен её центр и то, что она проходит через начало координат? Если можно, то каким образом?
- нет, нельзя;
- да, для этого потребуются дополнительные построения;
- да, потребуется составить уравнение данной окружности и всё сразу станет очевидно;
+ да, нужно подставить в уравнение окружности точку начала координат и получится искомый радиус.
