Тесты по геометрии 9 класс. Тема: "Синус, косинус, тангенс"
Правильный вариант ответа отмечен знаком +
1. Как называется раздел математики, изучающий функции синуса, косинуса, тангенса и их применение?
- геометрия
+ тригонометрия
- планиметрия
- стереометрия
2. Тригонометрические функции синуса и косинуса называются… тригонометрическими функциями. Вставьте пропущенное слов:
- обратными
- производными
+ прямыми
- основными
3. Выберите производную тригонометрическую функцию из предложенных:
- синус
- косинус
- арксинус
+ тангенс
4. С помощью какой фигуры определяются тригонометрические функции для острого угла?
+ прямоугольного треугольника
- равностороннего треугольника
- параллелограмма
- прямоугольника
5. Что такое синус острого угла?
- произведение двух прилежащих сторон в равностороннем треугольнике
+ отношение противолежащего катета в прямоугольном треугольнике к гипотенузе
- отношение прилежащего катета в прямоугольном треугольнике к гипотенузе
- отношение прилежащей стороны в параллелограмме к высоте, опущенной на эту сторону
6. Если в единичной полуокружности провести луч, который будет пересекать полуокружность в точке K. Чему будет равен синус угла, образованного лучом и осью абсцисс?
- абсциссе точки K
- единице
+ ординате точки K
- нулю
7. В каких пределах располагается значение синуса острога угла?
- от -1 до 0
- от -1 до 1
- от 0 до ∞
+ от 0 до 1
8. Может ли синус угла быть равен 0?
- может, если угол тупой
+ может, если угол равен 0° или 180°
- может, если угол равен 90°
- нет, не может
9. Дан треугольник FBK. Известно, что FB=14 см, BK=7 см. Найдите синус угла BFK.
- 2
+ 0,5
- 1,2
- 0,8
тест 10. На рисунке изображен треугольник DNL, у которого известны три стороны. Найдите синус угла DNL.
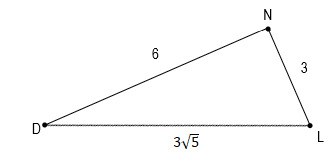
- 0,5
- 0
+ 1
- 3√5
11. На рисунке изображен ромб KEUT, диагонали которого пересекаются в точке O. Известно, что длина меньшей диагонали равна 6 см, большей диагонали – 8 см. Необходимо найти синус угла KET.
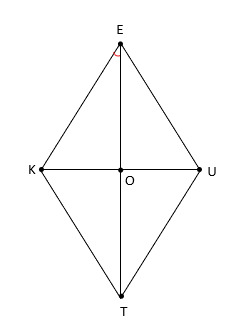
- 0,8
+ 0,6
- 0,5
- 0,2
12. Отношение прилежащего катета к гипотенузе в прямоугольном треугольнике называется… Закончите утверждение.
- котангенсом острого угла
- арккосинусом острого угла
+ косинусом острого угла
- арксинусом острого угла
13. Может ли косинус быть отрицательным?
- нет, не может
- может, если угол прямой
- может, если угол равен 0°
+ может, если угол тупой
14. Чему равен косинус прямого угла?
+ 0
- 1
- -1
- 0,5
15. В прямоугольном треугольнике прилежащий к углу α катет равен 2 см, противолежащий – 1 см, а гипотенуза равна 5 см. Чему равен косинус угла α?
- 0,2
- 0,5
+ 0,4
- 0,1
16. На рисунке изображена координатная плоскость с единичной полуокружностью. Координаты точки F равны (-0,7; 0,5). Найдите косинус угла α.
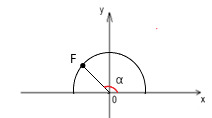
- 0
+ -0,7
- 0,5
- невозможно определить, так как косинус вычисляется только для острых углов в прямоугольном треугольнике
17. Выберите верную тригонометрическую формулу приведения:
- cos(90°−α) = sinα
- sin(90°−α) = cosα
- sin(180°−α) = sinα;
+ все перечисленные формулы являются формулами приведения
18. Косинус какого угла равен синусу 30°?
+ 60°
- 90°
- 30°
- 180°
19. Синус какого угла равен синусу 170°?
- 30°
- 180°
+ 10°
- синус не вычисляется для тупых углов
тест-20. Что такое тангенс острого угла в прямоугольном треугольнике?
- отношение прилежащего катета к противолежащему
+ отношение противолежащего катета к прилежащему
- отношение прилежащего катета к гипотенузе
- отношение противолежащего катета к гипотенузе
21. Как иначе можно найти тангенс угла?
- через отношение единицы к синусу угла
- через отношение косинуса угла к синусу
+ через отношение синуса угла к косинусу
- через отношение единицы к косинусу угла
22. С помощью какой таблицы можно определить значения основных тригонометрических функций?
- таблицы умножения
- таблицы Пифагора
- таблицы простых чисел
+ таблицы Брадиса
23. Известно, что FBXC – квадрат со стороной 17 см. Найдите тангенс угла XFB.
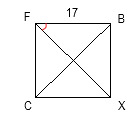
- √17
- 0,9
+ 1
- 0,5
24. Известно, что косинус угла равен 0,5. Определите тангенс этого угла.
+ √3
- 0,5
- 1
- 0
25. Выберите формулу основного тригонометрического тождества?
- sin²α - cos²α = 1
+ sin²α + cos²α = 1
- sin²α + cos²α = 0
- cos²α- sin²α = 1
26. Найдите, чему равно значение выражения 4sin(90°)α +3cos(0°).
- 7,5
- 5,5
+ 7
-5
27. Дан прямоугольный треугольник, в котором синус одного из углов равен 0,6. Найдите косинус этого угла.
+ 0,8
- -0,8
- 0,6
- -0,6
