Тесты - Угол между векторами. Скалярное произведение векторов, 9 класс с ответами

Тесты по геометрии 9 класс. Тема: "Угол между векторами. Скалярное произведение векторов"

Правильный вариант ответа отмечен знаком +

1. Дайте определение понятию «вектор»:

- отрезок, соединяющий две точки, расположенные в разных четвертях векторной плоскости

- прямая, проходящая через три равноудаленные точки

+ направленный отрезок, для которого указано, какая из точек является началом, а какая концом

- любая скалярная величина, выраженная положительным числом

2. Два вектора, которые … либо лежат на одной прямой, называются коллинеарными. Вставьте пропущенную фразу.

- перпендикулярны друг другу

- выходят из одной точки

- равны друг другу

+ параллельны одной прямой

3. Как называются векторы, которые являются противоположными противоположно направленным векторам?

- однонаправленные

- равнонаправленные

+ сонаправленные

- направленные в одну сторону

4. Какими являются векторы, изображенные на рисунке:

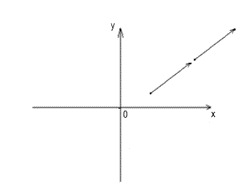
+ коллинеарными и сонаправленными

- коллинеарными и противоположно направленными

- неколлинеарными и равными

- равными и противоположно направленными

5. Кратчайший угол, на который нужно повернуть один вектор вокруг своего начала до положения сонаправленности с другим вектором называется:

-углом между векторами, выходящими из разных точек

+ углом между векторами, выходящими из одной точки

- углом между коллинеарными векторами

- углом между противоположно направленными векторами

6. Если угол между векторами равен 0^o, следовательно, векторы:

- неколлинеарные

- противоположно направленные

+ сонаправленные

- выходят из начала координат

7. Угол между противоположно направленными векторами равен:

- 90^o

- 0^o

+ 180^o

- 360^o

8. Как называются векторы, угол между которыми прямой?

- параллельными

+ перпендикулярными

- координатными

- осевыми

9. Дан ромб RHKF. Известно, что RH=RK. Найдите угол между векторами 

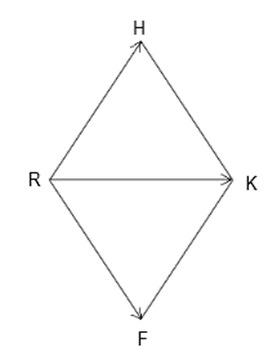
- 180^o

- 100^o

+ 120^o

- 360^o

тест 10. Как иначе называется длина вектора?

- расстояние

+ модуль

- отрезок

- размер

11. Как вычислить длину вектора, если известны его координаты?

+ она равна квадратному корню из суммы квадратов координат

- она равна произведению квадратов координат

- она равна отношению произведения координат к сумме их квадратов

- она равна сумме квадратов координат

12. Известно, что координаты вектора равны {-4; -6}. Найдите модуль вектора .

- 2√6

- 24

+ 2√13

- 52

13. Что такое скалярное произведение двух векторов?

- произведение координат векторов

- произведение квадратов длин этих векторов

- произведение квадратов модулей этих векторов на синус угла между ними

+ произведение модулей этих векторов на косинус угла между ними

14. В каком случае скалярное произведение ненулевых векторов равно нулю?

- если они коллинеарны

+ если они перпендикулярны друг другу

- если они сонаправлены

- если они противоположно направлены

15. Скалярное произведение векторов, изображенных на рисунке, будет:

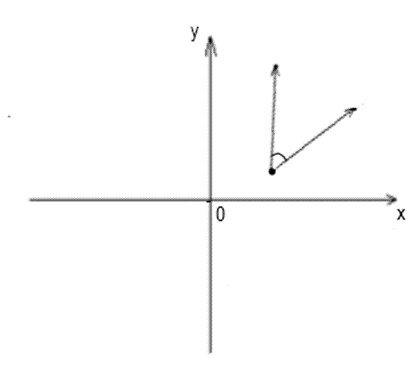
- равным единице

- равным нулю

- отрицательным

+ положительным

16. Может ли скалярное произведение векторов быть отрицательным числом?

- может, если один из векторов имеет отрицательные координаты

+ может, если угол между векторами тупой

- может, если вектора расположены в разных координатных четвертях

- не может

17. Чему равен косинус угла между векторами?

- сумме модулей векторов и их скалярного произведения

+ отношению скалярного произведения векторов к произведению их длин

- квадратному корню из скалярного произведения векторов

- произведению модулей векторов

18. Координаты двух векторов равны {3;4} и {4;3}. Необходимо найти косинус угла между этими векторами.

-0,95

- 1

- 0,76

+ 0,96

19. Дан прямоугольник GKVB. Известно, что длина вектора , а длина вектора  Найдите скалярное произведение этих векторов.

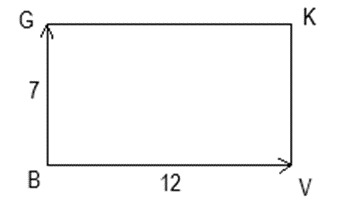
- 84

+ 0

- 193

- 1

тест-20. В треугольнике GBK стороны GB и BK равны, угол BGK=60^o, а сторона GK=6 см. Найдите скалярное произведение векторов 

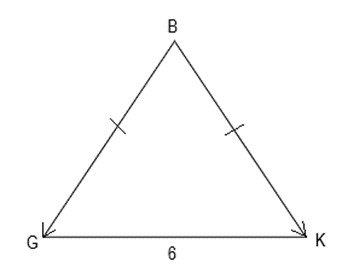
+18

- 0

- 36

- 46

21. Скалярное произведение векторов, выраженных своими координатами, вычисляется как:

- произведение всех координат на синус угла между векторами

- произведение квадратов всех координат

- квадратный корень из произведения их координат

+ сумма попарного произведения их координат

22. Даны два вектора с координатами. Вектор и вектор Найдите скалярное произведение этих векторов.

- 14

- 18

+ 34

-32

23. Даны три точки F, K и G с их координатами. По данным рисунка найдите косинус угла K.

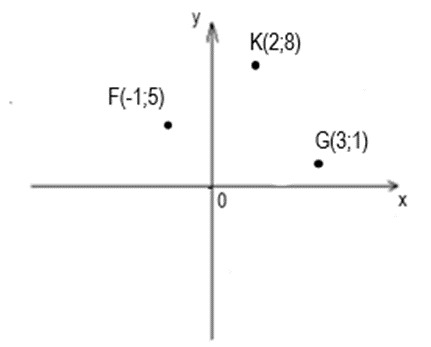
- 0

+ 0,6

- 1

- 0,5

24. Скалярный квадрат вектора равен… Закончите утверждение:

- произведению его координат

+ квадрату его длины

- квадратному корню из его модуля

- половине его длины, возведенной в квадрат

25. Выберите верное утверждение:

- скалярное произведение вектора самого на себя может быть отрицательным

- скалярное произведение вектора на самого себя не может быть равно нулю

+ скалярное произведение вектора самого на себя всегда больше или равно нуля

- все утверждения неверны

26. Найдите скалярный квадрат вектора с модулем 6 и координатами {4;3}.

- 12

- √6

+ 36

- 9