Тесты - Уравнения окружности и прямой 9 класс с ответами

Тесты по геометрии 9 класс. Тема: "Уравнения окружности и прямой"

Правильный вариант ответа отмечен знаком +

1. Пусть дана окружность с центром в точке D (d; g). Имеется, так же, еще одна точка окружности E(f; t). Тогда уравнение данной окружности с радиусом y будет таким:

+ (f-d)²+(t-g)²=y²;

- (f+d)²+(t-g)²=y²;

- (f-d)²+(t+g)²=y²;

- (f+d)²+(t+g)²=y².

2. Каково уравнение окружности, имеющей центр в начале координат, точкой D (d; g) и радиусом y?

- d²- g²=y²;

+ d²+g²=y²;

- d²+y²=g²;

- d²-y²=g².

3. Некоторая окружность имеет центр в точке F (5; 0). Каково уравнение этой окружности, если известно, что она так же проходит через начало координат?

- z²+5=0;

- z²-5=0;

+ (z-5)²+(x-0)²=25;

- z-5=25.

4. Можно ли найти радиус окружности, зная лишь то, что она проходит через начало координат и ее центр?

- нет;

- нужны дополнительные построения;

- данных для этого недостаточно;

+ конечно можно.

5. Известен центр окружности, а также есть данные о том, что она проходит через начало координат. Если ее центр в точке T (4; 0), то радиус будет равен…

- 16;

+ 4;

- 2;

- 5.

6. Среди представленных вариантов нужно выбрать тот, что указывает на верную запись уравнения прямой. При этом известно, что ее центр с координатами (3; 0). Она соприкасается с началом координатных осей.

- z²+6z-d²=0;

+ z²+6z+d²=0;

- z²+6z+d²=9;

- z²-6z-d²=3.

7. У окружности с центром в точке (8; 0) нужно найти радиус. Следует выбрать верный ответ, если известно, что окружность проходит через начало осей.

- 64;

- 16;

+ 8;

- 4.

8. Дана задача следующего содержания:

Окружность проходит через начало осей. Ее центр (9; 0). Нужно найти радиус ее.

Решение:

1) Запишем уравнение данной окружности

(с+9)²+(v-0)²=r²

2) Так как окружность проходит через начало координат, то уравнение преобразуется

(0+9)²+(0-0)²=r²

3) r=9

В каком из пунктов имеется ошибка или недочет?

+ 1;

- 2;

- 3;

- все пункты без ошибок.

9. Дано уравнение окружности: z²+s²=25. Нужно узнать принадлежит ли точка A (3; -4) этой окружности.

+ да;

- нет;

- нужны дополнительные построения;

- неизвестно.

тест 10. Если нужно узнать принадлежит ли точка уравнению, что нужно сделать?

- координаты точки подставить в уравнение окружности, потом проверить равны ли части уравнения, в том случае, если они равны – данная точка будет принадлежать окружности;

+ подставить координаты точки в уравнение окружности, а затем проверить равны ли обе части уравнения, если равны – точка принадлежит окружности;

- нужно оценить визуально принадлежит ли данная точка окружности;

- потребуется координаты точки подставить в имеющееся уравнение, если обе части не равны, следовательно, точка подтверждает свою принадлежность данной окружности.

11. Если есть окружность с радиусом 3, а также известно, что она проходит через начало осей, то ее уравнение будет иметь вид:

+ z²+q²=9;

- z²- q²= 9;

- z²+q²=3;

- z²-q²=3.

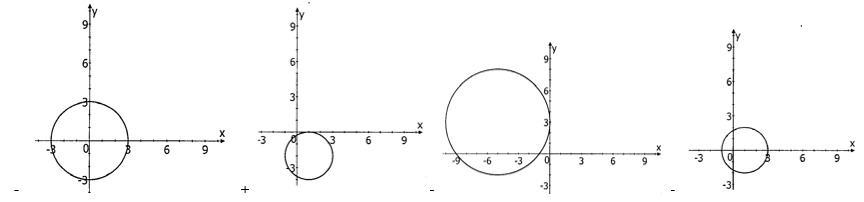
12. Дано уравнение (x-1)²+(y+2)²=4. Какая из представленных окружностей соответствует этому уравнению?

 

13. Дан рисунок. Среди представленных вариантов уравнений, нужно выбрать то, что соответствует данному изображению.

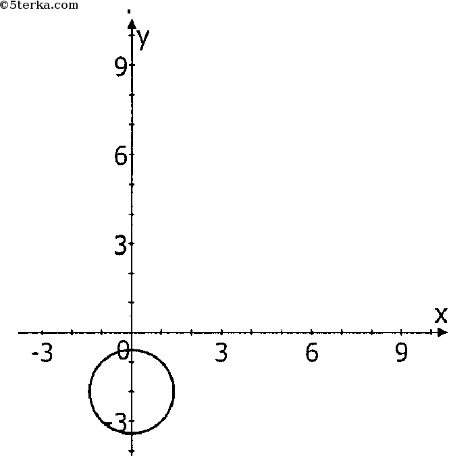
- x²-(y-2)²=2;

+ x²+(y+2)²=2;

- x²+(y+2)²=4;

- x²-(y-2)²=4.

14. Среди представленных вариантов выбрать тот, что показывает общий вид прямой в прямоугольной системе координат?

- ax²+by+c=0;

- ax²+by²+c=0;

+ ax +by +c=0;

- ax³+by+c=0.

15. Если требуется написать уравнение прямой, которая проходит через пару заданных точек, то нужно…

+ подставить их координаты в общий вид уравнения прямой, затем выразить через одно из уравнений коэффициенты и подставить их во второе уравнение;

- ничего делать не нужно – все и так понятно;

- подставить координаты точек в уравнение прямой и искомое уравнение найдено;

- записать общий вид уравнения прямой с подставленными в него координатами точек и сократить всё лишнее.

16. Даны две точки с координатами (1; -2) и (5; 6). Нужно составить уравнение прямой, которая будет проходить через эти две точки.

Решение:

1) Запишем уравнение прямой в общем виде

ax +by +c=0

2) Подставим каждую из точек в это уравнение

a -2b +c=0

5a+6b+c=0

3) Выразим а и b из одного уравнения

a=2b-c, b=c/4

4) Подставим во второе уравнение

c/2*x+c/4*y+c=0

Следует найти пункт с ошибкой.

- 2;

- 3;

- 4;

+ верного ответа нет.

16. Нужно выбрать уравнение прямой, содержащей точку (4; 6).

- 2a-6b+c;

+ 4a+6b+c;

- 2a-3b-c;

- a+b+c.

17. Дана прямая 4x+6y+1=0. Нужно выбрать из приведенных ниже примеров тот, который иллюстрирует пересечение ее с осью Ox.

+ 6y+1=0;

- 4x+6y-1=0;

- 4x+1=0;

- 4x+6y+1=0.

18. Имеется прямая следующего вида 6x-4y-1=0. Который из вариантов изображает пересечение этой прямой с осью Oy?

- 6x-4y-1=0;

- 6x-4y=0;

+ 6x-1=0;

- -4y-1=0.

19. Дан рисунок с изображенной на нем прямой. Какая из прямых там изображена?

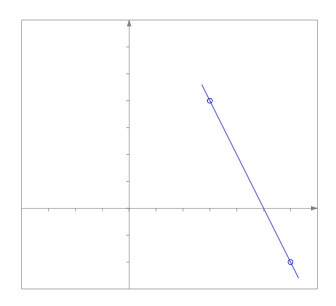
- 2x+2y=10;

- 2x-y-1=0;

- x-y-1=0;

+ -2x-y+10=0.

тест-20. Дана точка (-8; -6). Указать ее абсциссу.

+ -8;

- -6;

- 2;

- 4.

21. Есть точка (8; 7). Указать ее ординату.

- 8;

- 4;

+ 7;

- 0.

22. Если известно, что прямая пересекают одну из осей, что нужно делать в этом случае?

+ подставить в уравнение прямой нулевое значение вместо x или y;

- уравнение прямой останется неизменным;

- подставить в уравнение прямой любую точку;

- не стоит предпринимать какие-либо действия.

23. Какая из осей называется осью абсцисс?

- Oy;

+ Ox;

- Oz;

- нет верного варианта.

24. Какая из осей координат зовется осью ординат?

- Ox;

+ Oy;

- Oz;

- нет верного варианта.

25. Если нужно найти точки пересечения двух прямых, то:

- обязательно нужно их изобразить и сделать соответствующие выводы;

- нужно внимательно посмотреть на уравнения этих двух прямых и все сразу станет на свои места;

+ нужно выразить абсциссу и ординату через уравнения данных прямых;

- ничего не нужно делать, всё и так понятно.

26. Даны два уравнения прямых 4x+3y-6=0 и 2x+y-4=0. Какова точка их пересечения?

- (-9; -14);

+ (-9; 14);

- (9; 14);

- (14; -9).

27. Даны два уравнения прямых 5x+6y-7=0 и 2x+y+4=0. Нужно найти точки их пересечения.

Решение:

1) Выразим из второго уравнения y

y=-4-2x

2) подставим в первое уравнение

5x+6 (-4-2x) -7=0

x=35

3) y=4-2*35=66

Среди представленных пунктов нужно указать тот, который с ошибкой.

- 1;

+ 2;

- 3;

- все верные.

28. Если требуется найти точку пересечения двух прямых, то можно ли просто приравнять их уравнения друг к другу и искомая точка будет найдена?

- да;

+ нет;

- только в исключительных случаях;

- такое часто бывает.

29. Дано уравнение 4x-5y-2=0. Указать точки, принадлежащие ей.

- (-1; 1);

- (1; 0);

- (4; 5);

+ (3; 2).

тест_30. Чтобы найти точку, принадлежащую прямой нужно обязательно…

- начертить прямую;

+ подставить в уравнение прямой любую точку и если равенство будет верным, следовательно, точка принадлежит прямой;

- нужно долго подготавливаться к построению прямой и прямоугольной системы координат;

- очень внимательно посмотреть на уравнение прямой и сделать верные выводы.