Тесты по геометрии 8 класс. Тема: "Прямоугольник"
Правильный вариант ответа отмечен знаком +
1. Что называют прямоугольником?
- фигура, у которой имеются равные углы и равные стороны;
- фигура с параллельными противоположными сторонами;
- четырёхугольник с попарно параллельными и равными сторонами;
+ четырехугольник, у которого противоположные стороны равны и параллельны, а углы прямые.
2. Ниже приведены геометрические фигуры. Среди них нужно выбрать прямоугольник.

3. Какое определение справедливо для противоположных сторон прямоугольника:
- если стороны являются продолжением друг друга, то они считаются противоположными;
+ стороны, не имеющие точек соприкосновения, называются противоположными;
- равные стороны, принято считать противоположными;
- говорят, что если начало одной стороны начинается от конца второй, то они будут противоположными.
4. Какой из рядов с составляющими элементами прямоугольника верный?
- 4 равных стороны, 4 угла;
- 5 сторон, 5 углов, 1 угол прямой;
+ 4 стороны, 4 прямых угла;
- прямой угол, 2 острых угла, 4 стороны.
5. Свойство, характерное для прямоугольника:
- противоположные стороны не равны;
- диагонали разделяются на три части при пересечении;
- стороны, расположенные рядом равны;
+ стороны, лежащие напротив одинаковы.
6. Среди представленных свойств следует выбрать верное для прямоугольника.
+ диагонали параллелограмма с прямыми углами при пересечении делятся пополам;
- если имеются в прямоугольнике диагонали, то они непременно делятся на множество равных частей;
- среди имеющихся диагоналей обязательно есть та, что больше другой;
- диагонали в параллелограмме с прямыми углами равны, но не всегда.
7. Следует завершить высказывание: «Если фигура, называемая параллелограммом, имеет одинаковые диагонали, то...»
+ данная фигура называется прямоугольником;
- данный параллелограмм является правильным;
- данная фигура будет четырехугольником;
- она параллелограмм с диагоналями.
8. Сколько на рисунке прямоугольников и как он (они) называются?
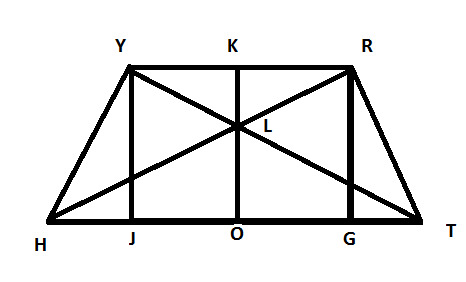
- один, JYRG;
- два, JYRG, JYKO;
+ три, JYRG, JYKO, OKRG;
- четыре, JYRG, OKRG, JYKO.
9. Прямоугольник – это … многоугольник. Следует выбрать верное слово на месте пропуска.
- невыпуклый;
+ выпуклый;
- не достаточно сведений для выбора;
- сложно сказать.
тест 10. Если в прямоугольнике сложить все углы, то их сумма будет равняться:
+ 360°;
- 180°;
- 270°;
- 450°.
11. Верно ли, что если хоть один угол в параллелограмме прямой, то он считается прямоугольником?
- да;
+ нет;
- некорректный вопрос;
- затрудняюсь ответить.
12. Сколько должно быть прямых углов в параллелограмме, чтобы его считали прямоугольником?
- 1;
- 2;
+3;
-0.
13. Что нужно сделать для нахождения периметра прямоугольника?
- перемножить все стороны между собой;
- перемножить соседние стороны, а затем сложить полученный результат;
- сложить смежные стороны, а потом умножить результат;
+ сложить все стороны между собой.
14. Дан прямоугольник HJKL. Его диагонали пересекаются в точке D. Длина диагонали HK равна 14 см. Угол KHL равен 30°. Каков будет периметр данного прямоугольника?
+ 2√147+14;
-√147+14;
- 2√147;
- 3√147+14.
15. В прямоугольнике DFGH проведены диагонали. Угол GDH имеет величину 30°. Значит ли это, что весь угол D будет равняться 60°?
- да;
+ нет;
- нельзя сказать, не измерив его величину;
- не могу сказать.
16. Чему будет равняться сумма величин соседних углов в прямоугольнике?
- 90°;
+180°;
- 127°;
-145°.
17. Периметр прямоугольника равен 56 см. Одна из сторон равна 8 см. Требуется отыскать значение смежной стороны.
- 16;
-28;
-36;
+20.
18. Даны две стороны прямоугольника. Их длины 3 дм и 5 дм. Среди представленных вариантов выбрать верный, содержащий периметр данной фигуры.
+16;
-64;
-12;
-15.
19. Необходимо вычислить периметр прямоугольника QSXC, если в нём из угла Q проведена биссектриса. Причём биссектриса QH делит сторону SX на отрезки 2 дм и 4 дм.
- 12;
- 14;
- 18;
+16.
тест-20. PNWR – прямоугольник. PK – биссектриса угла Р. PK делит WR на некоторые отрезки, длиной 1 см и 3 см. Периметр данного прямоугольника равняется:
+10;
- 4;
- 5;
-8.
21. Если в прямоугольнике проведена биссектриса к одной из сторон, какое следствие из этого вытекает?
+ биссектриса поделит угол, из которого выходит, пополам, а, следовательно, образует равнобедренный прямоугольный треугольник;
- биссектриса не делит угол, из которого выходит, пополам, а значит образуется прямоугольный треугольник;
- никакое следствие не вытекает;
- биссектриса отсекает еще один прямоугольник в уже имеющемся.
22. В прямоугольнике LPOI известна сторона LP. Она равна 14 см. Угол LPI = 60°. PI и LO являются диагоналями. Каково значение стороны LO?
+ 28;
- 14;
- 24;
- 26.
23. Имеется прямоугольник UASM. Он состоит из двух других прямоугольников с разными периметрами. Это прямоугольники UAKN и NKSM. В UAKN известна сторона UA=3 см и периметр. Он равен 36 см. Известно, так же, что UN=1,5 UM. Требуется найти периметр прямоугольника NKSM. В приведенном ниже решении нужно указать этап с ошибкой.
Решение:
P – периметр UAKN. Он равен 36 см.
36=2*(3+х)
36=6+х
30=2х
х=15
UN=1,5 UM=3*1,5=4,5 см
PNKSM = (4,5 +3)*2=15 см.
Варианты ответов:
- 1;
+ 2;
- 3;
- все этапы решены верно.
24. Если прямоугольник составлен из нескольких прямоугольников, то его периметр можно найти:
+ сложив периметр этих прямоугольников;
- сложив их боковые стороны;
- перемножив их периметры;
- умножив длины оснований друг на друга.
25. В прямоугольнике OLKM проведены диагонали. Они пересекаются в точке J. Угол JOM равен 38°. Нужно найти угол OJM.
- 90°;
- 76°;
-102°;
+ 104°.
26. Какие выводы можно сделать при проведении в прямоугольнике двух диагоналей?
+ диагонали образуют четыре равнобедренных треугольника;
- они делят фигуру на четыре остроугольных треугольника;
- диагонали дают возможность работать с четырьмя равными треугольниками;
- нет верного умозаключения.
27. Есть фигура с параллельными противоположными сторонами и четырьмя прямыми углами. В ней проведены диагонали. Одна из диагоналей образует со стороной угол в 52°. Какое умозаключение будет верным, в связи с данными сведениями?
- все углы образованного треугольника будут острые;
- один из углов нового треугольника тупой;
- все углы в новообразованном треугольнике тупые;
+ один из углов полученного треугольника будет острым.
28. При пересечении двух диагоналей треугольника появляются четыре треугольника. Что можно о них сказать?
- ничего;
- появляются четыре равносторонних треугольника;
+ образуются четыре равнобедренных треугольника;
- строятся несколько разносторонних фигур.
29. На рисунке изображён прямоугольник с диагоналями. Что можно сказать, глядя на рисунок?
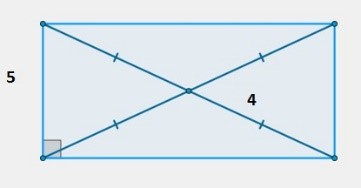
- все стороны равны 5, а диагонали 4;
- все стороны равны;
- все диагонали равны между собой и имеют величину 4;
+ диагонали делятся при пересечении поровну на отрезки равные 4, боковые стороны равны 5.
тест_30. Можно ли прийти к верному заключению о том, что перед нами прямоугольник, зная лишь то, что он имеет четыре прямых угла?
- да;
+ нет;
- трудно сказать;
- верного заключения не выйдет.
