Тесты по геометрии 8 класс. Тема: "Площадь трапеции"
Правильный вариант ответа отмечен знаком +
1. Площадь практически любой трапеции (не имеющей прямые углы) является возможным найти, разделив на некоторые фигуры:
+ два треугольника и прямоугольник;
- один треугольник и квадрат;
- один прямоугольник и треугольник;
- два квадрата.
2. Площадь каждой трапеции – это...
- поверхность, составленная из квадратов;
- поверхность, обнесённая треугольником;
+ часть поверхности, ограниченная двумя параллельными и двумя не параллельными прямыми;
- участок поверхности, ограниченный парами взаимно параллельных прямых.
3. Площадь прямоугольной трапеции можно вычислить, если поделить поверхность фигуры на несколько частей. Они будут являться:
- ромбом и треугольником;
- треугольниками;
- квадратами;
+ прямоугольником и треугольником.
4. Для вычисления площади трапеции, нужно:
+ умножить половину суммы оснований на высоту трапеции;
- разделить пол суммы оснований на высоту;
- умножить одно из оснований на высоту;
- разделить меньшее основание на высоту трапеции.
5. Прямоугольная трапеция имеет меньшее основание длиной 6 см. Меньшая боковая сторона тоже равна 6 см, а тупой угол имеет значение 135°. Требуется указать верную площадь.
- 108;
- 36;
- 9;
+ 54.
6. Есть трапеция с прямым углом. Её высота делит большее основание на отрезки 3,3 см и 1,7 см. Тупой угол равен 135°. Требуется выяснить длину высоты и меньшего основания данной трапеции?
- высота 3,3, а основание 1,7;
+ основание 3,3, а высота 1,7;
- высота 1,7, а основание 5;
- основание 3, 3, а высота 5.
7. Большее основание равнобедренной трапеции разделено высотой на два отрезка длиной 4 см и 2 см. Самый большой угол равен 135°. Чему будет равняться площадь фигуры?
- 9;
- 12;
+ 8;
- 24.
8. Основания трапеции равны 10 см и 6 см. Высота равна 4 см. Необходимо посчитать площадь данной трапеции.
- 16;
- 18;
- 24;
+ 32.
9. Высота трапеции равна половине длины меньшего основания. Основания равны 16 см и 12 см. Требуется указать верное значение площади трапеции.
- 28;
- 56;
- 20;
+ 84.
тест 10. Дан рисунок. Указать верное значение средней линии трапеции.
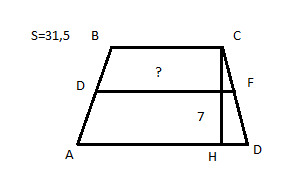
+ 4,5;
- 9;
- 7;
- 8.
11. Дана средняя линия трапеции, длиной 7 см. Высота равна 3 см. Площадь этой фигуры имеет следующее значение:
- 9,5;
+ 21;
- 49;
- 63.
12. Каким образом можно найти площадь трапеции?
- умножив любое из оснований на высоту;
- умножив боковую сторону на высоту;
- поделив среднюю линию трапеции на высоту;
+ умножив среднюю линию трапеции на высоту.
13. Требуется определить по рисунку, какая прямая будет являться средней линией трапеции:
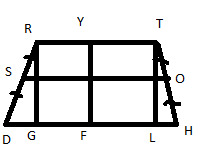
+ SO;
- RG;
- TL;
- YF.
14. В прямоугольной трапеции нужно найти острый угол, если даны длины оснований 5 и 13, а площадь 81.
+ 45°;
- 35°;
- 55°;
- 65°.
15. Известна площадь трапеции. Она равна 64. Имеется, также, средняя линия, равная 8. Тогда высота данной трапеции будет:
+ 8;
- 64;
- 16;
- 24.
16. Одно из оснований трапеции меньше средней линии в 3 раза. Во сколько раз больше величина средней линии длины второго основания?
- в 10 раз;
- в 3 раза;
+ в 5 раз;
- в 1,5 раза.
17. Требуется завершить высказывание: Прямая, проходящая через середины оснований, разбивает её на ... с одинаковыми площадями
- 4 равновеликих части;
- 3 равных части;
+ 2 равновеликих части;
- 2 разные фигуры.
18. Следует завершить предложение: Диагонали трапеции делят её на ... треугольника.
+ 4;
- 2;
- 3;
- 5.
19. В трапеции KLOP отрезок FG соединяет середины оснований. Получаются две новые трапеции KLFG и GFOP. Будут ли равны их площади?
- нет;
- нужно делать дополнительные построения, чтобы понять;
+ да;
- неизвестно.
тест-20. По рисунку определить отношение площадей треугольников WOE и QOR.
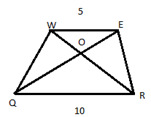
- 2;
+ 4;
- 1/2;
- 1/4.
21. Чему равна средняя линия трапеции?
+ полусумме оснований;
- сумме оснований;
- произведению оснований;
- половине произведения оснований.
22. Так как диагонали трапеции делят её на подобные треугольники, то их сходственные стороны относятся друг к другу в соответствии с:
- квадратом коэффициента подобия;
- признаками равенства треугольников;
+ коэффициентом подобия;
- признаками равенства фигур.
23. При разделении трапеции диагоналями получаются треугольники. Они подобны и их площади равны:
- коэффициенту подобия;
- большему основанию;
- меньшему основанию;
+ квадрату коэффициента подобия.
24. Как изменится площадь трапеции, если её большее основание увеличить в 2 раза?
- увеличится в 2 раза;
- уменьшится в 1,5 раза;
- уменьшится в 2 раза;
+ увеличится в 1,5 раза.
25. Каким образом поменяется площадь трапеции, если её высоту уменьшить в 3 раза?
+ уменьшится в 3 раза;
- увеличится в 3 раза;
- уменьшится в 2 раза;
- увеличится в 2 раза.
26. Какие изменения произойдут с площадью трапеции, если меньшее основание увеличить в 2 раза, а большее основание уменьшить в 5 раз.
- увеличится в 2 раза;
- уменьшится в 2 раза;
+ площадь останется той же;
- площадь уменьшится в 2,5 раза.
27. При пересечении двух диагоналей трапеции образуются подобные треугольники. Как изменится коэффициент подобия, если большая сторона трапеции выросла в 4 раза?
- не изменится;
- уменьшится в 2 раза;
- увеличится в 2 раза;
+ увеличится в 4 раза.
28. В трапеции две диагонали пересекаются, образуя подобные треугольники. Что произойдёт с коэффициентом подобия, если большая сторона уменьшится в 4 раза.
+ ничего не произойдёт;
- увеличится в 4 раза;
- уменьшится в 4 раза;
- уменьшится в 2 раза.
29. Дан рисунок. Известно расстояние между прямыми a и b. Оно равно 7. Основания равны 3 и 5. Площадь этой трапеции равна:
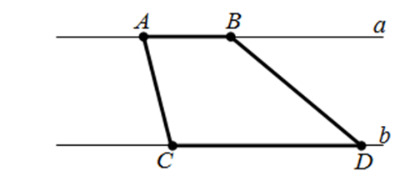
- 30;
+ 28;
- 15;
- 21.
тест_30. Дана трапеция. Известно расстояние от одного основания до другого. Оно равно 6, а длина самих оснований 7 и 5. Площадь равна...
- 72;
- 56;
+ 36;
- 42.
