Тесты - Подобие треугольников 8 класс с ответами

Тесты по геометрии 8 класс. Тема: "Подобие треугольников"

Правильный вариант ответа отмечен знаком +

1. На рисунке изображены две похожие фигуры. В каком из вариантов они будут подобными?

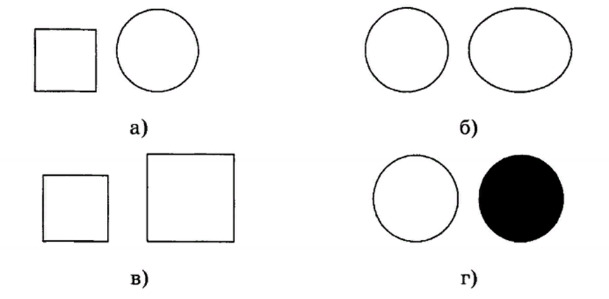
- а;

- г;

- б;

+ в.

2. Отношение сторон одного треугольника было задано как 2:4:6. Меньшая из сторон, подобного ему второго треугольника, равняется 4 см. Определите, чему будет равняться периметр этого треугольника.

- 18 см;

- 22 см;

- 20 см;

+ 24 см.

3. Сколько подобных треугольников изображено на этом рисунке?

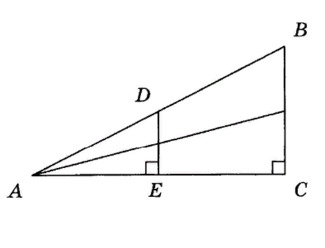
- 2;

- 4;

- 1;

+3.

4. Треугольники KLM и K₁L₁M₁ подобны. Известно, что отношение площади треугольника KLM к площади K₁L₁M₁ равно 3. Чему равно отношение сходственных сторон KL к K₁L₁?

+ √3;

- 3;

- 6;

- 9.

5. Сходственные стороны треугольников MKE и M₁K₁E₁ равны соответственно 9 и 3. Площадь треугольника MKE равна 27. Чему равняется площадь треугольника M₁K₁E₁?

- 27;

- 9;

- √27;

+ 3.

6. Отношение площадей подобных треугольников ABC и MNL равно 81. Сторона АВ равна 18. Найдите длину сходственной ей стороны MN.

- 0,22;

- 4,5;

+ 2;

- 9.

7. Стороны треугольников KLM и FER равны: KL = 5, LM = 2, MK = 4; FE = 2,5, ER = 1, RF = 2. Подобны ли данные треугольники? Если да, чему равняется коэффициент подобия?

- треугольники не будут подобными;

+ треугольники подобны, их коэффициент подобия 2;

- они будут подобными, коэффициент подобия 3;

- треугольники являются подобными, с коэффициентом подобия 5.

8. В треугольнике ABC угол А = 80°, угол B=15°, сторона АВ = 3. В треугольнике A₁B₁C₁ угол В₁ = 80°, угол С₁=85°, сторона A₁B₁ равна 9. Являются ли треугольники ABC и A₁B₁C₁ подобными? Почему?

- не являются, так как не справедлив ни один из признаков подобия;

+ являются, так как 2 угла 1-го треугольника соответственно равны 2-м углам другого треугольника;

- являются, так как 2 стороны одного треугольника пропорциональны 2-м сторонам другого треугольника, а углы между этими сторонами равны;

- являются, так как 3 стороны одного треугольника пропорциональны 3-м сторонам другого треугольника.

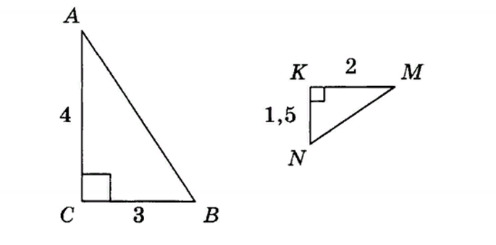
9. Подобны ли равнобедренные треугольники, приведённые на рисунке?

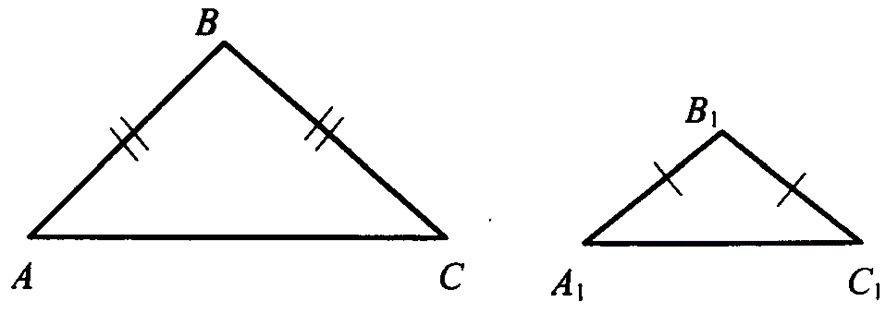
- Треугольники не являются подобными;

- треугольники являются подобными по 2-м пропорциональным сторонам и равным углам между ними;

+ треугольники являются подобными по 2-м равным углам;

- в условии не хватает данных для решения задачи.

10. Треугольники KLM и K₁L₁M₁ подобны. Площадь треугольника KLM меньше площади треугольника K₁L₁M₁ на 5 единиц. Коэффициент подобия равен √6. Чему равна площадь треугольника KLM?

- 5*√6;

- 5: √6;

- 7;

+2.

11. Дана задача: «Треугольники MKE и M₁K₁E₁ подобны. MK = 4, KE = 5, EM=3. Коэффициент подобия равен 2 (треугольник M₁K₁E₁ больше). Найдите отношение периметров этих треугольников». Ниже приведено ее решение. В одном из этапов допущена ошибка. В ответе укажите номер этого этапа.

Решение:

1) Периметр треугольника MKE = MK + KE + EM = 4 + 5 + 3 = 12.

2) Так как треугольники подобны, стороны треугольника M₁K₁E₁ можно найти по формулам:

M₁K₁ = MK/2 =4/2=2;

K₁E₁ = KE/2=5/2=2,5;

E₁M₁ = EM/2=3/2=1,5.

3) Периметр треугольника M₁K₁E₁ = M₁K₁ + K₁E₁ + E₁M₁ = 2 + 2,5 + 1,5 = 6.

4) Отношение периметров треугольников MKE и M₁K₁E₁ равно 12:6=2.

Выберите правильный ответ:

-1;

+2;

- 3;

- 4.

12. Имеются подобные треугольники MKE и M₁K₁E₁. Причем, MK = 4, KE = 5, EM=3. Известен коэффициент подобия данных треугольников. Он равен 2, M₁K₁E₁ - больший треугольник. Требуется найти отношение периметров рассматриваемых треугольников.

+2;

- 4;

- 6;

- 8.

13. На рисунках изображены два треугольника. Являются ли они подобными? Если да, чему равен коэффициент подобия? Учитывайте размер клеток на рисунках - 1х1.

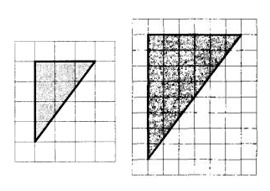
- треугольники подобными не будут;

- треугольники считаются подобными, коэффициент подобия 1,5;

+ треугольники подобные, с коэффициентом подобия 2;

- треугольники подобные, их коэффициент подобия 4.

14. Треугольники ABC и LRE подобны: MN = средняя линия в треугольнике ABC. Найдите коэффициент подобия треугольников LRE и MBN.

+1,5;

- 2;

- 4;

- эти треугольники не будут подобными.

15. В треугольнике EDF был проведён отрезок MN параллельно отрезку DF. Чему будет равен коэффициент подобия получившихся треугольников, если известно, что длина EN = 4 см, а NF= 1 см.

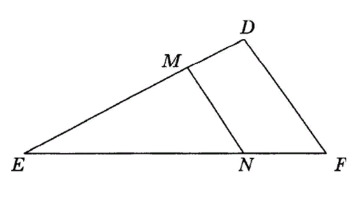
- 4;

- 1/4;

- 5;

+ 4/5 или 5/4.

16. В прямоугольном треугольнике ABC провели отрезок MN, перпендикулярный гипотенузе AB. Какое утверждение будет верным?

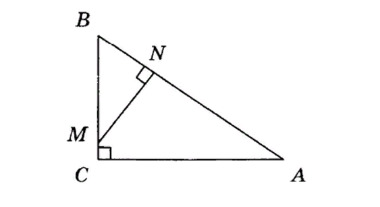
Треугольники ABC и MNB будут:

- подобными по 2-м пропорциональным сторонам, а также углу между ними;

- они подобные по паре сторон;

- не подобные;

+ подобные по паре углов.

17. Ученик 8 класса средней школы, ростом 1 м 75 см, стоит рядом со столбом. Длина тени школьника равняется 95 см, а длина тени столба составляет 3 м 80 см. Чему будет равна высота столба?

- 7 м;

- 6 м 95 см;

- 7 м 10 см;

+ 7 м 40 см.

18. Треугольники ABC и AB1C подобны, а отрезки AB и A1B1 являются сходственными сторонами. Чему будет равно отношение ?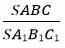

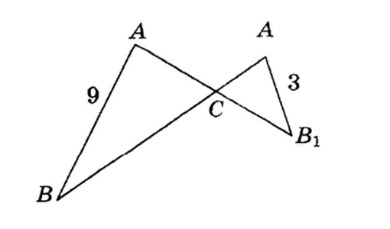
- 6;

- 3;

- 2;

+ 9.

19. В треугольнике ABC биссектриса CD проведена из угла C. Какое равенство будет верным?

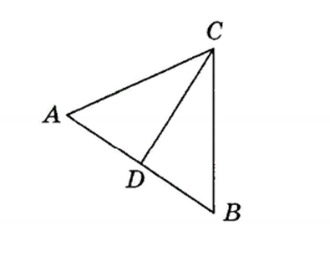
- AC/CD= CD/DB;

- AD/DC= CD/DB;

- AC/CB= DB/AD;

+ AD/BD= AC/BC.

20. На рисунке изображены подобные отрезки. Какое из выражений будет верным для этих отрезков?

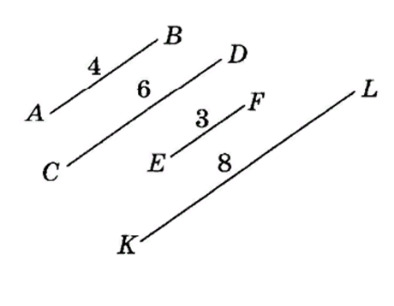
- KL/EF= CD/AB;

- AB/CD= EF/KL;

-AB/EF= CD/KL;

+CD/KL= EF/AB.

21. В треугольнике ABC были проведены высоты BB₁ и CC₁. Назовите подобный треугольник для треугольника ABB₁.

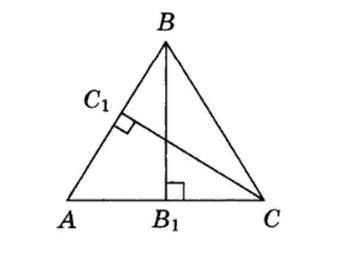
- BB₁C;

- BC₁C;

- CC₁B;

+ ACC₁.

22. Чему будет равна длина основания AD у трапеции ABCD?

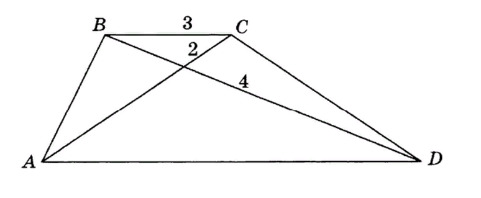
- 4;

- 8;

- 12;

+ 6.

23. Дана равнобедренная трапеция ABCD, в которой диагональ AC перпендикулярна боковой стороне CD, а сторона BE перпендикулярна диагонали AC, E принадлежит AC. Длина основания трапеций равняется 6 см и 10 см. Необходимо определить соотношение AE:EC.

- 1:3;

- 3:2;

- 3:1;

+ 2:3.

24. В треугольнике ABC проведена средняя линия XY. Длина отрезка AB = 8 см. Чему будет равна длина отрезка XY?

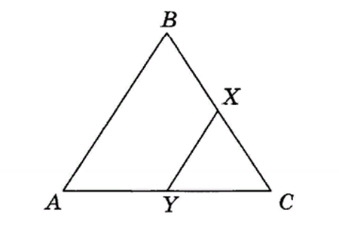
- 2 см;

- 1 см;

- 6 см;

+ 4 см.

25. Выберите верное соотношение между элементами треугольника ABC

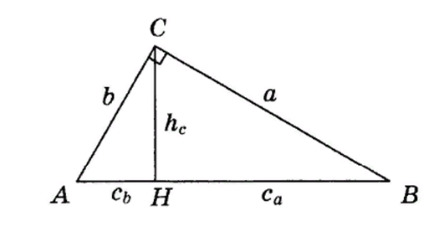
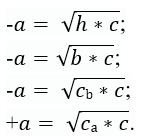
26. На рисунке изображены два подобных треугольника. Чему равен отрезок MN?

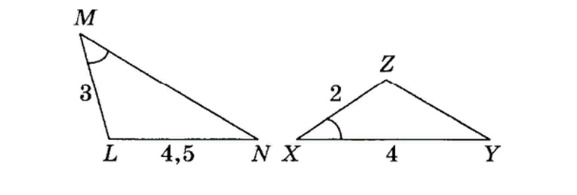
- 5;

- 4;

- 9;

+ 6.

27. На рисунке изображены два треугольника ABC и MNK. Эти два треугольника считаются подобными. Какому углу соответствует угол A первого треугольника?

- ∠ B;

- ∠ N;

- ∠ K;

+ ∠ M.

28. Согласно признакам подобия, два треугольники подобны, если:

- в треугольниках имеются равные углы;

- у каждого из треугольников стороны пропорциональны сходственным сторонам другого;

- они равны;

+ у этих треугольников углы соответственно равны, а стороны пропорциональны сходственным сторонам другого.

29. Отрезки АВ и СК пропорциональны отрезкам МР и ЕО, если:

- АВ : ЕО = СК : МР;

- АВ : МР = ЕО : СК;

- АВ : СК = ЕО : МР;

+ АВ : МР = СК : ЕО.

30. Треугольник АВС подобен треугольнику А₁В₁С₁, АВ = 4 см, ВС = 6 см, АС = 7 см, А₁В₁ = 8 см. Чему равна сторона В₁С₁?

- 14 см;

- 3 см;

- 3,5 см;

+ 12 см.