Тесты по геометрии 8 класс. Тема: "Площадь треугольника"
Правильный вариант ответа отмечен знаком +
1. AC – гипотенуза, длина стороны 7 см. Длина высоты BH, проведенной к AC 4 см. Найти площадь треугольника.
1) 28 см2 -
2) 7 см2 -
3) 14 см2 +
4) 22 см2 -
2. В треугольнике с площадью 5 см2 к стороне BC=4 см проведена высота. Найдите её длину.
1) 2 см -
2) 2,5 см +
3) 4 см -
4) 5,5 см -
3. Площадь прямоугольного треугольника KAB 15 см2. Найдите высоту, проведенную к AB=5 см.
1) 8 см -
2) 6 см +
3) 2 см -
4) 4 см -
4. Найдите площадь треугольника, стороны которого равны 9, 12 и 15 см.
1) 81 см2 -
2) 72 см2 -
3) 108 см2 -
4) 54 см2 +
5. Сторона треугольника CAE AE равна 6 см, EC = 3 см. Высота к AE равна 4 см. Найдите длину высоты к CE.
1) 2 см -
2) 8 см +
3) 4 см -
4) 12 см -
6. Катеты прямоугольного треугольника соответственно равны 6 и 8 см, необходимо найти его площадь.
1) 48 см2 -
2) 24 см2 +
3) 28 см2 -
4) 100 см2 -
7. Высота треугольника ABC равна той же в треугольнике KZL. Каково отношение площадей данных треугольников, если длины оснований высот относятся как 1:3?
1) 1:3 +
2) 1:1 -
3) 1:6 -
4) 1:2 -
8. К гипотенузе треугольника проведена высота длиной 4 см. Найти длину гипотенузы, если площадь треугольника равна 12 см2.
1) 6 см +
2) 3 см -
3) 8 см -
4) 2 см –
9. Площадь BPD 24 см2. В треугольнике проведена медиана BE. Площадь треугольника BEP равна:
1) 12 см2 +
2) 18 см2 -
3) 8 см2 -
4) 16 см2 -
тест 10. Найти сторону равностороннего треугольника, если его площадь равна 4√3 см2.
1) 3√3 см -
2) 4 см +
3) √3 см -
4) 2 см –
11. Найти сторону треугольника, если известна его площадь S=84 см2 и длины двух других сторон: 13 см, 15 см.
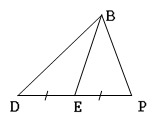
1) 11 см -
2) 7 см -
3) 14 см +
4) 21 см –
12. Площадь треугольника на рисунке равна:
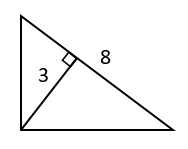
1) 11 см2 -
2) 12 см2 +
3) 14 см2 -
4) 24 см2 -
13. Длины сторон и высоты представлены на рисунке. Найти длину неизвестной стороны.
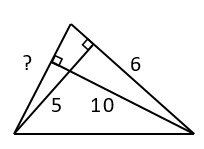
1) 8 см -
2) 6 см -
3) 3 см +
4) 1 см -
14. Катеты прямоугольного треугольника соответственно равны 6 и 11 см. Найти площадь треугольника.
1) 66 см2 -
2) 33 см2 +
3) 30 см2 -
4) 60 см2 -
15. Исходя из рисунка, высоты треугольников равны. Длина высоты 6 см. площадь меньшего треугольника 24 см2. Найдите площадь большего треугольника, если известно, что основания высот относятся как 1:1.5.
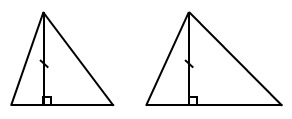
1) 24 см2 -
2) 30 см2 -
3) 36 см2 +
4) 42 см2 -
16. Площадь треугольника KLH 18 см2. Найдите площадь треугольника KLM, если известно, что LH – медиана.
1) 18 см2 -
2) 24 см2 -
3) 27 см2 -
4) 36 см2 +
17. Вычислите площадь равностороннего треугольника со стороной 6 см.
1) 12 см2 -
2) 9√3 см2 +
3) 6√3 см2 -
4) 9 см2 -
18. Найти площадь треугольника, если известно, что EH – высота, EH=7 см, DK=12 см.
1) 38 см2 -
2) 42 см2 +
3) 76 см2 -
4) 84 см2 -
19. Вычислите площадь треугольника.
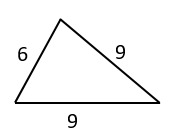
1) 36 см2 -
2) 36√2 см2 -
3) 18 см2 -
4) 18√2 см2 +
тест-20. Площадь прямоугольного треугольника 20 см2. Найти длину катета AC, если длина катета AB=8 см.
1) 2 см2 -
2) 4 см2 -
3) 5 см2 +
4) 8 см2 -
21. Найти площадь треугольника.
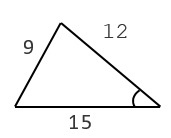
1) 54 см +
2) 51 см -
3) 108 см -
4) 83 см –
22. На гипотенузу ED=12 см опущена высота AK=8 см. Вычислите площадь прямоугольного треугольника AED.
1) 96 см2 -
2) 72 см2 -
3) 48 см2 +
4) 24 см2 -
23. Треугольник ABC – равнобедренный. В нём проведены две высоты. Длина высоты, проведённой к боковой стороне BC равна 12 см. Высота, опущенная к основанию треугольника AC=15 см, имеет длину 10 см. Найти длину боковой стороны.
1) 12 см -
2) 12,5 см +
3) 14 см -
4) 15,5 см –
24. В равностороннем треугольнике проведена высота. Найти площадь треугольника EKL, если площадь треугольника EKP=14 см2.
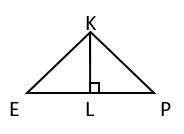
1) 10 см2 -
2) 9 см2 -
3) 7 см2 +
4) 8 см2 -
25. Площадь треугольника 40 см2. Найти длину его стороны, если на неё опущена высота, длиной 8 см.
1) 6 см -
2) 8 см -
3) 10 см +
4) 12 см -
26. Найти AK, если известно, что KE=10 см, EA=6 см, площадь треугольника AKE равна 24 см2.
1) 6 см -
2) 8 см +
3) 10 см -
4) 12 см -
27. В треугольниках EDM и SNP проведены высоты EK и SA, причём EK=SA=7 см. Найти длину NP, если известно, что она в 2,5 раза больше DM, и площадь EDM равна 28 см2.
1) 18 см -
2) 20 см +
3) 24 см -
4) 28 см -
28. Вычислить длину стороны равностороннего треугольника с площадью √3 см2.
1) √3 см -
2) √3/2 см -
3) 1 см +
4) 1/2 см -
29. Вычислить длину второго катета, если площадь треугольника 35 см2.
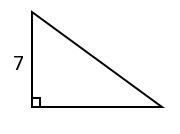
1) 5 см -
2) 8 см -
3) 10 см +
4) 11 см -
тест_30. В треугольнике BAK проведены две высоты: BH=8 см и AC=4 см. Найти длину KA, если известно, что площадь треугольника равна 12 см2, BK=6 см.
1) 2 см -
2) 3 см +
3) 5 см -
4) 6 см -
31. AC=7 см, BH=12 см. Найти площадь ΔAMC.
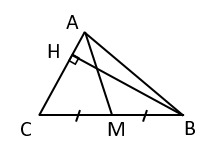
1) 18 см2 -
2) 19 см2 -
3) 21 см2 +
4) 24 см2 -
32. Найти площадь треугольника, в котором к стороне AC=3 см проведена высота BK=6 см.
1) 6 см2 -
2) 9 см2 +
3) 12 см2 -
4) 18 см2 –
