Тесты по геометрии 7 класс. Тема: "Первый признак равенства треугольников"
Правильный вариант ответа отмечен знаком +
1. Правильно завершите следующую фразу: "Первый признак равенства треугольников - это признак равенства ..."
- Всех сторон и углов, имеющихся у треугольника;
+ Угла между обеими сторонами;
- Трех сторон;
- Нет верного ответа.
2. Правильное ли утверждение, что в случае, когда угол и стороны любого треугольника равен обеим сторонам и углам другого треугольника, то такие треугольники равные?
- Правильное;
+ Неправильное;
- Смотря какой вид треугольника;
- Нет правильного ответа.
3. В треугольниках ABC и MNK AB = MN. ∠B = ∠N. Какое еще условие должно выполняться, чтобы треугольники были равными за первым признаком?
- BC = MN;
+ BC = NK;
- AC = MK;
- AC = NK.
4. В треугольниках MNK и DЕF MK = DF, а MN = DЕ. Равность каких сторон или углов нужно восстановить, чтобы получить результат о равенстве треугольников по первому признаку?
- ∠N = ∠Е;
- ∠K = ∠F;
+ ∠M = ∠D;
- NK = ЕF.
5. В треугольниках ABC и A1B1C1 AB = A1B1, AC = A1C1, ∠A = ∠A1, ∠В = ∠В1. Какое из условий, представленных ниже, лишнее для равенства треугольников по первому признаку?
- ∠A = ∠A1;
+ ∠В = ∠В1;
- АС = А1С1;
- АВ = А1В1.
6. Опираясь на рисунок, определить какая сторона считается противоположной углу А в этом треугольнике.
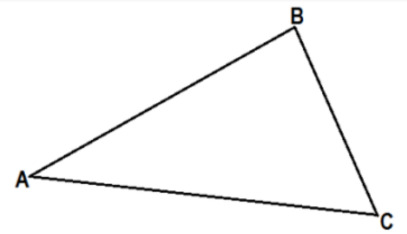
- АС;
- АВ;
+ ВС;
- Невозможно определить.
7. Треугольник АВС - равносторонний, АВ = 5 см. Вычислите какой периметр имеет треугольник АВС.
+ 15 см;
- 5 см;
- 20 см;
- 30 см.
8. Определите тип треугольника со сторонами 6 см, 6 см и 7 см.
- Равносторонний;
- Прямоугольный;
+ Равнобедренный;
- Разносторонний.
9. Дайте полное и правильное определение треугольнику.
+ Геометрическая фигура, у которой есть три угла и три стороны;
- Геометрическая фигура, у которой все стороны равны и каждый угол имеет 90 градусов;
- Четырехугольник, все стороны которого параллельны;
- Параллелограмм, у которого все стороны равны.
тест 10. Определите тип треугольника, который имеет углы 60, 80 и 40 градусов.
- Прямоугольный;
- Тупоугольный;
- Разносторонний;
+ Остроугольный.
11. Перпендикуляр, проведенный из вершины треугольника к противоположной стороне, называется…
+ Высотой треугольника;
- Медианой треугольника;
- Биссектрисой треугольника;
- Стороной треугольника.
12. Какие элементы принадлежат треугольнику?
- Медиана;
- Биссектриса;
- Высота;
+ Все вышеперечисленные элементы.
13. Две фигуры называются равными, если они:
- Имеют равные периметры;
- Имеют равные площади;
+ Совмещаются при наложении;
- Имеют одинаковую форму.
14. Как называется треугольник, если градусная мера одного из углов равняется 90 градусам?
- Остроугольный;
+ Прямоугольный;
- Тупоугольный;
- Развернутый.
15. Выберите из ниже предложенных предложений неверное утверждение.
- Треугольник — это замкнутая двумерная форма с тремя прямыми сторонами;
+ Треугольник не считается многоугольником;
- Острый треугольник имеет внутренние острые углы с менее чем 90 градусов, а прямоугольный имеет только один прямой угол, который равен 90 градусам;
- Тупоугольный треугольник имеет один угол (с более 90 градусами).
16. В треугольниках ABC и MNK АВ = MN, ВС = NK, ∠В = ∠N. За каким признаком можно доказать равенство этих треугольников?
+ За первым признаком;
- За вторым признаком;
- За третьим признаком;
- Доказать невозможно.
17. Продолжите фразу: "Если два треугольника равны, то элементы (стороны, углы, медианы, биссектрисы, высоты и тому подобные) одного из них соответственно равны ..."
+ Элементам второго;
- Только углам второго;
- Только медианам второго;
- Только высотам второго.
18. Выберите НЕ верное продолжение утверждения: "Два прямоугольных треугольника равны, если выполняется одно из условий ниже"
- Катет и острый угол одного треугольника соответственно равняются катету и острому углу другого треугольника;
- Гипотенуза и острый угол одного треугольника равняются гипотенузе и острому углу другого треугольника;
- Гипотенуза и катет одного треугольника равняются гипотенузе и катету другого треугольника;
+ Катет и острый угол одного треугольника соответственно равняются гипотенузе и катету другого треугольника.
19. Определите, какой из ниже предложенных вариантов НЕ считаются признаками равнобедренного треугольника:
- Два угла равны;
+ Высота и биссектриса совпадают;
- Медиана и стороны совпадают;
- Медиана и высота совпадают.
тест-20. Укажите правильное название и полную подпись к рисунку.
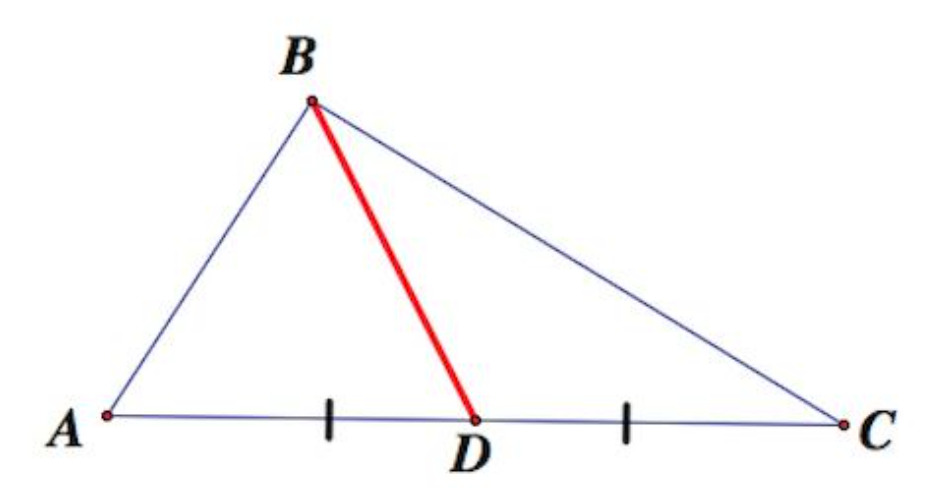
- Треугольник АВС с высотой ВD;
+ Треугольник АВС с медианой ВD;
- Треугольник АВСD;
- Четырехугольник АВСD.
21. Укажите неправильное утверждение:
- Любой треугольник можно классифицировать по внутренним углам, измеренным в градусах;
- Каждый прямоугольный треугольник имеет 90 градусов в одном из внутренних углов;
- Сторона, противоположная прямому углу - это гипотенуза, которая считается самой длинной стороной любого треугольника;
+ Помимо гипотенузы, остальные две части называются вершинами.
22. Отрезок ВМ - биссектриса треугольника АВС. Найдите градусную меру угла АВС, если угол АВМ = 30°.
- 90°;
- 30°;
+ 15°;
- 60°.
23. Найдите угол С, если углы А и В по 70°.
- 70°;
- 180°;
- 40°;
+ 140°.
24. Один из углов треугольника равен 40°, а второй втрое меньший от третьего. Найдите неизвестные углы треугольника.
+ 35°и 105°;
- 40°и 40°;
- 90°и 60°;
- 180°и 140°.
25. Найдите каждый угол треугольника (равнобедренный), когда угол при основе на 30 меньше от угла при вершине.
- 60°, 60°и 30°;
- 120°, 180°и 180°;
- 30°, 180°и 120°;
+ 4°, 70°и 70°.
26. Угол между высотой СН и катетом СА прямоугольного треугольника АВС (угол АСВ = 90°) равен 15°. Найдите острые углы треугольника АВС.
- 30°;
+ 15°;
- 90°;
- 60°.
27. Угол между биссектрисой ВМ и АС (катет) АВС (прямоугольный треугольник) равен 62°. Найдите острые углы треугольника АВС.
- 56°;
- 35°;
+ 34°;
- 90°.
28. Найдите угол А, если угол С - 50°.
+ 100°;
- 70°;
- 180°;
- 50°.
29. Один из углов треугольника равняется 54°, пока второй в два раза меньший от третьего. Определите сколько градусов у остальных углов треугольника.
- 126°и 180°;
+ 42° и 84°;
- 60° и 90°;
- 90° и 90°.
тест-30. Выберите какое предложение неверное:
- Треугольник всегда можно разделить на два прямоугольника;
- Треугольники - это многоугольники с наименьшим количеством точек и сторон;
- Чтобы классифицировать треугольники по углам и сторонам, измеряются внутренние углы и длина всех сторон.
+ Некоторые типы треугольников не имеют в сумме 180 градусов.
