Тесты - Сложение и вычитание многочленов 7 класс с ответами

Тесты по алгебре 7 класс. Тема: "Сложение и вычитание многочленов"

Правильный вариант ответа отмечен знаком +

1. Перед сложением или вычитанием каждый многочлен нужно:

- разложить на множители;

+ привести к стандартному виду;

- преобразовать в одночлен;

- возвести в степень.

2. Какой этап лишний при выполнении сложения (вычитания) многочленов:

- записать операцию, поместив многочлены в скобки и поставив между ними нужный знак;

- раскрыть скобки с учетом знаков перед ними;

- привести подобные члены;

+ представить результат в виде одночлена.

3. Упрости выражение (12x – 35y) – (4x – 23y):

- 8x + 12y;

- 8x – 58y;

+ 8x – 12y;

- 16x – 58y.

4. После приведения подобных членов в выражении (1 – x²) + (2x – 7) + (x² – 3)

- 2x² + 2x + 11;

+ 2x – 9;

- 3x² – x – 3;

- 4x – 9.

5. Алгебраическая сумма многочленов 5,4х – 3,5х² и 2,45х² – 1,6х равна:

+ 3,8х – 1,05х²;

- 7,85х – 5,1х²;

- 4,8х – 1,95х²;

- 1,05х² + 3,8х.

6. Разность многочленов 0,75a² – 2,25b² и 1,5b² + 0,23a² равна:

- -0,75a² – 2,02b²;

+ 0,52a² – 3,75b²;

- 0,98a² – 2,02b²;

- 0,98a² – 3,75b²;

7. Если к многочлену 2х + 5 – 2у прибавить 1, то получится:

- 3х + 5 – 2у;

+ 2х + 6 – 2у;

- 2х + 5 – у;

- 2х + 5 – 3у.

8. Что получится в результате сложения двух противоположных многочленов?

+ 0;

- 1;

- одночлен;

- многочлен.

9. Разность многочлена 2х² – 5х + 6 с противоположным ему многочленом будет равна:

- 0;

- 10х;

+ 4х² – 10х + 12;

- 4х² – 10х.

тест 10. При сложении многочлена 7x² + 2y² – 5 с противоположным ему выражением получится:

+ 0;

- 14x² + 4y² – 10;

- 1;

- x² + y² – 1.

11. Чтобы привести многочлен 2х + 3у – 5 + х + 2у – 7 к стандартному виду, нужно:

- разложить его на слагаемые, взяв многочлены в скобки;

- сложить все числовые значения;

+ привести подобные члены;

- перемножить все числовые и буквенные значения.

12. После приведения многочлена 2х + 3у – 5 + х + 2у – 7 к стандартному виду получится выражение:

- (2х + 3у – 5) + (х + 2у – 7);

+ 3х + 5у – 12;

- 20ху;

- 8ху – 12.

13. В записи многочленов (7_ + 3_ - 10_) и (13_ - 17_ - 2_) пропущены буквенные значения х², х и у. Известно, что при их сложении получился многочлен 5х² + 16у – 27х. Что это за многочлены?

- 7у + 3х² – 10х и 13х – 17у – 2х²;

+ 7х² + 3у – 10х и 13у – 17х – 2х²;

- 7у + 3х – 10х² и 13 х – 17х² – 2у;

- 7х + 3х² – 10у и 13х² – 17х – 2у.

14. В записи многочленов (5_ - 7_ + 11_) и (-2_ + 7_ - 9_) пропущены буквенные значения х, ху и у. Разность этих многочленов представлена в виде многочлена 20ху – 5у – 2х. Что это за многочлены?

+ 5х – 7у + 11ху и -2у + 7х – 9ху;

- 5у – 7х + 11ху и -2х + 7у – 9ху;

- 5х – 7у + 11ху и -2х + 7у – 9ху;

- 5у – 7х + 11ху и -2у + 7х – 9ху.

15. Рассмотри рисунки и скажи, какое выражение показывает, на сколько вторая фигура больше первой:

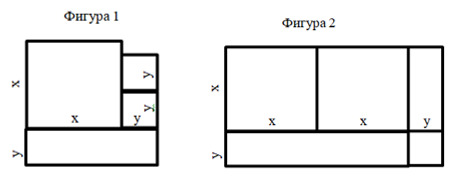
+ x² - 2y² + 2xy;

- -2y² + 2x² - 3xy;

- 3x² + 4y² + 4xy;

- x² - 4y² + 2xy.

16. Площадь какой из фигур можно представить в виде многочлена, получившегося при сложении двух многочленов: 3х² – 2у² – 2ху и 5у² – 4х² + ху?

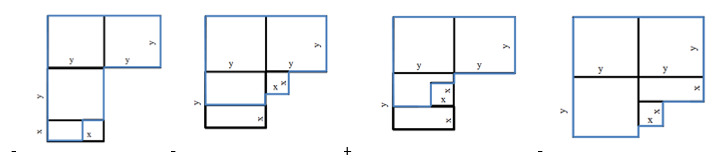
17. Чему равна сумма многочленов 2х² + 3ху – 275х + 26у – 14у² и 14у² – 26у – 3ху + 275х – 2х²?

+ 0;

- 4х² + 6ху – 550х + 52у – 28у²;

- 6ху – 275х + 26у – 28у²;

- 4х² – 28у².

18. Если упростить выражение (2 + 3х²) – (х² – 2х + 3) – (х³ + х), то получится многочлен вида:

- х² – 2х + 5;

- х³ + 4х² – 3х + 5;

+ -х³ + 2х² + х – 1;

- -х³ + 2х² – х + 1.

19. Многочлен х² – ху² + 3х²у + 2у² был образован в результате сложения многочленов:

- (5х²у – 2ху² + 2х² – 2у²) + (2х²у + 3ху² – х² + 4у²);

+ (х²у – 3ху² + 2х² – у²) + (2х²у + 2ху² – х² + 3у²);

- (2х²у – ху² + 2х² – у²) + (4х²у + 2ху² – 2х² + 3у²);

- (2х²у – 5ху² + х² – у²) + (х²у + 4ху² – 2х² + 3у²);

тест-20. Значение выражения (0,75х – 0,26у) – (0,25х – 0,06у) + (0,6х – 0,1у) при х=2, у=6 равно:

- 1,4;

- -0,32;

- -0,58;

+ 0.4.

21. Решением уравнения (4х + 37) – (2х – 16) = 63является число:

+ 5;

- 21;

- 3,5;

- 58.

22. Многочлен 5х + 3у получился в результате разности многочленов:

- 3х + 2у и 2х – у;

+ х² – 3х + у и х² – 8х – 2у;

- 6х – 3у и х + 6у;

- 2х – у и 3х + 4у.

23. Сумма многочленов 3х + 2у и 2у – 5х равна разности многочленов:

- 3х – 3у и х + у;

- х – 3у и х + у;

+ 5х + 5у и 7х + у;

- 2х + у и 4х + 3у.

24. Если упростить выражение – (2х + 2,5у) + (х – 1,75у), то получится многочлен:

+ 0,75у – х;

- 3х + 0,75у;

- х + 0,75у;

- 0,75у – 3х.

25. Многочлен 2х + 5у – 7 получился в результате выполнения математических действий с выражениями:

- (х + 2у – 5) – (х + 3у – 2);

+ (3у – х – 2) + (2у + 3х – 5);

- (у + 2х + 3) – (4у – 4х + 4);

- (3х + 6у + 1) – (х + у – 6).

26. В каких выражениях результатом выполнения математических операций будет одночлен:

- (6х + 3у – 2ху) – (6х – 3у + 2ху);

- (3у – 5х – ху) + (3у - 5х + ху);

+ (2х – 5у + 7) – (2х – 5у + 2);

- (х + у – 2) + (х + у – 2).

27. Выбери такой многочлен, чтобы его сумма с многочленом 3х² – 2х + 7 была равна 2х² – х + 2:

+ х – х² – 5;

- х² + х – 5;

- 5 – х – х²;

- х – х² + 5.

28. Выбери такой многочлен, чтобы его разность с многочленом х + 3у была равна 3х – 2у + 1:

- 2у – 2х – 1;

+ 4х + у + 1;

- 2х + у + 1;

- 4х – у – 1.

29. После преобразования выражения (3х² – 5у + 1) – (2х² + 2у – 2) в многочлен стандартного вида, получается:

- х² – 3у – 1;

- х² + 3у + 1;

- х² – 7у – 1;

+ х² – 7у + 3.

тест_30. Если выражение 2х² – 1 представить в виде суммы двучленов, то оно может иметь вид:

- (2х² + 7) + (х² – 8);

- (х² – 3) + (х² + 4);

- (3х² – 2) + (3 – х²);

+ (2х² – 3х) + (3х – 1).

31. Если многочлен 3х + 7у представить в виде разности двучленов, то он может иметь вид:

+ (2х + 8у) – (у – х);

- (4х – 2у) – (х – 5у);

- (х + 3у) – (2х + 4у);

- (2х + 5у) – (2у – х).

32. В каком случае разность многочленов не будет представлена выражением 2х – 15:

- (3х + 27) – (х + 42);

- (х² + 2х) – (х² + 15);

+ (х² +2х + 7) – (х² – 8);

- (14 – 5х) – (29 – 7х).

33. Какой многочлен нужно прибавить к выражению 7х + 2у – 5, чтобы в результате получился одночлен?

+ 3у – 7х + 5;

- 7х – 5;

- 3х + 2у +5;

- х – 2у – 5.

34. Результатом сложения трех многочленов 3х² – 5х + 7, - х² + х – 2 и х² + 3х – 3 будет выражение:

- 5х² + 9х + 12;

+ 3х² – х + 2;

- х² – х + 5;

- 2х² + х – 2.

35. Какой многочлен нужно вычесть из выражения 5х – 2у + 13, чтобы результат делился на 5 без остатка при любом значении переменной:

- 3х + 2у – 2;

- х + 3у + 5;

+ 13 – 2у – 5х;

- у – 2х + 7.

36. В каком выражении после приведения подобных членов все числовые множители делятся на 3:

- (3х + 2у) – (х + у);

- (2х – 2у) + (х – 2у);

- (3х + у) – (х + 2у);

+ (2х – у) – (2у – х).

37. P₁ = 3х + 2у; P₃ = х + 3у; P₁ + P₂ = P₃. P₂ = ? (P – обозначение многочлена)

+ у – 2х;

- 2х + у;

- 4х – у;

- 4х + 5у.

38. P₁ = 3x – 5y; P₃ = 2x – 2y; P₁ – P₂ = P₃.

P₂ = ?

- 5х – 7у;

- х – 7у;

- 3у – х;

+ х – 3у.

39. После приведения подобных слагаемых в выражении (12x – 3y + 7z) – (5x + 2y + 3z) получится многочлен стандартного вида:

+ 7x – 5y + 4z;

- 7x – y + 10z;

- 7x – y + 4z;

- 7x – 5y + 10z.

тест*40. В каком случае представлен многочлен стандартного вида:

- (2х + 3у) – (у – х);

+ 2х + 3у – 7;

- 3х – у + 2х – 3;

- (5х + 2х) + (у – 3у) + (2 + 4).