Тесты - Многогранники 10 класс с ответами

Тесты по геометрии 10 класс. Тема: "Многогранники"

Правильный вариант ответа отмечен знаком +

1. Основания призмы все лежат в плоскостях:

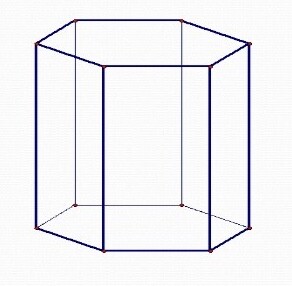
- в противоположных

- в математических

+ в параллельных

- в любых

2. Укажите, какое самое маленькое число ребер может содержаться в призме?

+ 9

- 6

- 3

- 12

3. Закончите предложение: Многоугольники в основании усечённой пирамиды…

- равные

+ подобные

- схожие

- любые

4. Выражение: «сумма трех измерений квадрата равна квадрат диагонали» принадлежит тому свойству параллелепипед

- Прямому параллелепипеду

- Параллелепипеду

+ Прямоугольному параллелепипеду

- Треугольному параллелепипеду

5. Шесть углов и шесть треугольников, этот многогранник –

- усечённой пирамидой

- шестиугольной призмой

- параллелепипед

+ шестиугольная пирамида

6. Какие равносторонние фигуры входят в тетраэдер:

-Пятиугольники

+ Треугольники

- Шестиугольники

- Четырехугольники

7. В каком многогранники нет центра симметрии:

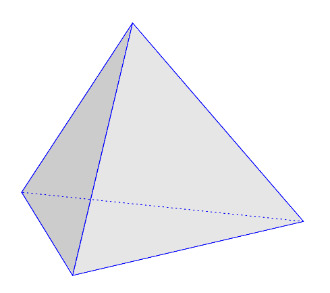
- Гексаэдр

+ Тетраэдр

- Икосаэдр

- Параллелепипед

8. Фигура: четырехугольная призма, основание – параллелограмм:

- квадрат

+параллелепипед

- параллелограмм

- ничего из предложенного

9. Многогранники могут быть:

- прямые/ непрямые

- вогнутые/ невогнутые

+ выпуклые/невыпуклые

- правильные/ неправильные

тест 10. Выберите правильный вариант ответа

+ концы ребер многоугольника называют вершинами

- концы ребер многоугольников называют основой

- началом ребер многоугольников называют вершинами

- началом ребер многоугольников называют основанием

11. Основание призмы:

- скрещиваются

+ параллельны и равны

- пересекаются и равны

- скрещиваются и равны

12. Призма, в которой боковые ребра параллельны ее высоте:

- у наклонной

+ у прямой

- у четырехугольной

- у трехугольной

13. Прямой треугольник с катетами 8 и 6 см – основание. Отыщите площадь боковой поверхности призмы, учитывая, что, если самая большая боковая грань – квадрат.

- 220 см²

- 260 см²

+ 240 см²

- 280 см²

14. Прямоугольный треугольник с гипотенузой 13 см и катетом 12 см – основание прямо призмы. Необходимо найти площадь боковой поверхности призмы, меньшая грань – квадрат.

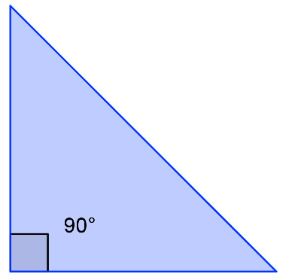
+ 150 см²

- 200 см²

- 240 см²

- 180 см²

15. Боковое ребро правильной четырехугольной пирамиды равно 4 см и образует с плоскостью основания пирамиды угол 45°. Найдите площадь боковой поверхности пирамиды и высоту пирамиды

- 18 √3 см² и 2√2 см

+ 16√3 см² и 2√2 см

- 20√3 см² и 2√4 см

- 14 √3 см² и 2√2 см

16. √6 см - высота правильной четырехугольной пирамиды. Боковое ребро наклонено к плоскости основания под углом 60°.

-7√2 см и 4√7 см²

+2√2 см и 4√7 см²

- 9√2 см и 4√9 см²

- 2√2 см и 4√3 см²

17. Ребро правильного тетраэдра DABC равно а. Нужно построить сечение тетраэдра, которое будет проходить через середину ребра DA параллельно плоскости DBC. Найдите площадь сечения.

+ (a2√3)/16

- (a2√3)/8

- (a2√9)/16

- (a4√3)/16

18. Ребро правильного тетраэдра DABC равно а. Нужно построить сечение тетраэдра, которое будет проходить через середину ребра АВ и DA параллельно ребру ВС. Найдите площадь сечения.

- (a4√3)/6

+ (a2√3)/16

- (a2√3)/8

- (a2√9)/16

19. Ромб с диагоналями 10 и 24 см - основание прямого параллелепипеда. Меньшая диагональ параллелепипеда образует с плоскостью основания угол 45°. Необходимо найти полной поверхности параллелепипеда.

- 770 см²

+ 760 см²

- 780 см²

- 800 см²

тест-20. Ромб с меньшей d 12 см - основание прямого параллелепипеда.Самая большая d параллелепипеда - 16√2 см, с боковым углом получается 45°. Необходимо найти полной поверхности параллелепипеда.

+640 см²

- 740 см²

- 840 см²

- 1000 см²

21. Пусть основание пирамиды правильный треугольник с S 9√3 см². Перпендикулярные 2 боковых грани пирамиды к плоскости основания. Третья грань наклонена под углом 30°. Вычислите S боковой поверхности пирамиды и найдите длины боковых ребер пирамиды.

- 32см²

+ 36см²

- 18 см²

- 38 см²

22. Если основание пирамиды равнобедренный прямоугольный треугольник с гипотенузой - 4√2 см. Боковые грани, содержащие катеты треугольника перпендикулярны плоскостям основания, третья грань была наклонена под углом 45°.Вам необходимо высчитать S боковой поверхности пирамиды и отыскать длины боковых ребер пирамиды.

- √4 см²

- √2 см²

+ 16√2 см²

- 9√8 см²

23. А - ребро куба ABCDA1B1C1D1. проходит сквозь прямую В1С и середину ребра AD. Выложите сечение куба, проходящее через прямую В1С и середину ребра AD, вычислите S сечения.

-8а2/8

- а2/8

+9а2/8

- 8а2/4

24. Ребро куба ABCDA1E1C1 равно а. Выстройте сечение куба, проходящее через точку С и середину ребра AD параллельно прямой DA1. S этого сечения?

+ 9а2/8

- 8а2/8

-18 а2/8

- а2/8

25. Основание прямой призмы — прямоугольный треугольник с катетами 15 и 20 см. Вычислите S полной поверхности призмы, если ее наименьшее сечение, проходящее через боковое ребро, — квадрат.

+25 см

- 14 cм

- 20 см

- 30 см

26. Основание прямой призмы — равнобедренный треугольник с основанием 24 см и боковой стороной 13 см. Наименьшее сечение призмы, проходящее через ее боковое ребро, является квадратом. Найдите S полн. поверхн. призмы.

- 120 см²

+ 370 см²

- 200 см²

- 250 см²

27. Основание пирамиды — ромб с большей диагональю d и острым углом α. Все двугранные углы при основании пирамиды равны β. Найдите S полной поверхности пирамиды.

- (D6/2*tg a) / 2 *(1: cos B + 1)

+ (D2/2*tg a) / 2 *(1: cos B + 1)

- (D2/2*tg a) / 2 *(4: cos B + 1)

- (D2/2*tg a) / 2 *(1: cos B + 2)

28. Основание пирамиды — ромб с тупым углом α. Все двугранные углы при основании пирамиды равны β. Найдите S полной поверхности пирамиды, если ее высота равна Н.

- ((4H2 ctg4 B)/ sin A) * (1+(1/ cos B))

- ((4H2 ctg2 B)/ sin A) * (1+(3/ cos B))

+ ((4H2 ctg2 B)/ sin A) * (1+(1/ cos B))

- ((4H4 ctg2 B)/ sin A) * (1+(1/ cos B))

29. Ребро куба ABCDA1B1C1D1 равно а. Постройте сечение куба, проходящее через середины ребер АА1, В1С1 и CD, и найдите площадь этого сечения.

- (3√3 * a2)/6

+ (3√3 * a2)/4

-(3√8 * a2)/4

-(8√3 * a2)/4

тест_30. Ребро куба ABCDA1B1C1D1 - а. Постройте сечение куба, проходящее через середины ребер А1В1, СС1 и AD, и найдите площадь этого сечения.

- (9√3 * a2)/4

- (6√3 * a2)/4

- (3√3 * a2)/2

+ (3√3 * a2)/4