Тесты по геометрии 10 класс. Тема: "Параллельность прямых и плоскостей"
Правильный вариант ответа отмечен знаком +
1. Какими называют плоскость и прямую, не имеющих ни одной общей точки?
- перпендикулярными
- скрещивающимися
+ параллельными
- прямыми
2. Посмотрите на рисунок и выберите правильное утверждение:
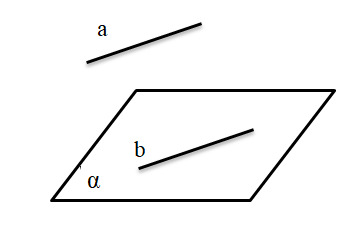
- Прямая а и плоскость α являются перпендикулярными.
- В плоскости α находится прямая а.
- Плоскость α и прямая b являются перпендикулярными.
+ Плоскость α и прямая а являются параллельными друг другу.
3. Сколько случаев взаимного расположения прямой и плоскости в пространстве имеется?
- один
- два
+ три
- четыре
4. В каком варианте ответа указано правильное суждение?
- Не находящаяся в данной плоскости прямая считается параллельной этой плоскости, если она пересекается с какой-либо прямой, находящейся на этой плоскости.
+ Если прямая не принадлежит данной плоскости и является параллельной какой-либо прямой на этой плоскости, то она считается параллельной данной плоскости.
- Не находящаяся в данной плоскости прямая, которая является параллельной лежащей на этой плоскости прямой, считается перпендикулярной данной плоскости.
- Если прямая не принадлежит данной плоскости и является перпендикулярной какой-либо лежащей на этой плоскости прямой, то она считается параллельной данной плоскости.
5. Через сколько точек можно провести лишь одну плоскость?
- одну
- две
+ три
- невозможно провести только одну плоскость
6.Если прямая K и плоскость α обладают одной общей точкой, то это значит, что:
- плоскость α и прямая K характеризуются параллельностью между собой.
+ плоскость α и прямая K пересекаются.
- прямая K находится в плоскости α.
- прямая K параллельна другой прямой, лежащей в плоскости α.
7. Плоскости S и T пересекаются третьей плоскостью U. Из этого следует, что:
- плоскости S и T перпендикулярны плоскости U.
- плоскости S и U являются параллельными.
- плоскости T и U являются параллельными.
+ линии пересечения плоскостей являются параллельными.
8. Выберите правильное утверждение:
+ При условии, что плоскость проходит через данную прямую, являющуюся параллельной другой плоскости, и пересекает эту плоскость, то линия пересечения плоскостей всегда параллельна данной прямой.
- Чтобы линия пересечения плоскостей была параллельна прямой, плоскость должна проходить через прямую, являющуюся перпендикулярной другой плоскости, и пересекать эту плоскость.
- Если линия пересечения плоскостей параллельна данной прямой, то плоскость проходит через эту прямую, являющуюся параллельной другой плоскости, и не пересекает эту плоскость.
- Чтобы линия пересечения плоскостей была перпендикулярна прямой, плоскость должна проходит через прямую, являющуюся параллельной другой плоскости, и пересекать эту плоскость.
9. Каких плоскостей называют параллельными?
- перпендикулярных
- пересекающихся
- прямых
+ не пересекающихся
тест 10. Даны две параллельные между собой прямые Y и Z. Одна из них, а именно прямая Z, параллельна данной плоскости. Значит, прямая Y:
- не принадлежит данной плоскости или является ей перпендикулярной.
- и данная плоскость являются скрещивающимися или она лежит в этой плоскости.
+ находится в данной плоскости или параллельна этой плоскости.
- параллельна данной плоскости или не лежит этой плоскости.
11. У плоскости α и прямой D множество общих точек. Это обозначает, что:
- плоскость α и прямая D являются перпендикулярными.
- плоскость α и прямая D пересекаются в одной точке.
- прямая D и плоскость α параллельны между собой.
+ прямая D находится в плоскости α.
12. В плоскости α лежит основа BC треугольника ABC. Точка P является серединой основы BC. Выберите правильное суждение:
- Прямые AP и BC являются параллельными.
- Прямая AP и плоскость α являются параллельными.
+ Прямая CP находится в плоскости α.
- Прямые AP и BC не пересекаются.
13. В каких случаях плоскостей можно считать параллельными?
+ При условии, что две находящиеся в одной плоскости пересекающиеся прямые параллельны двум лежащим в другой плоскости пересекающимся прямым.
- При условии, что две лежащие в разных плоскостях параллельные прямые перпендикулярны двум находящимся в другой плоскости параллельным прямым.
- При условии, что две пересекающиеся и находящиеся в одной плоскости прямые перпендикулярны двум лежащим в другой плоскости пересекающимся прямым.
- При условии, что одна находящаяся в одной плоскости прямая пересекается с другим лежащим в другой плоскости прямым.
14. Есть три плоскости F, L, O. Плоскость F является параллельной плоскости O, плоскость L – параллельной плоскости O. Исходя из этого выберите правильное утверждение:
- Плоскость F и плоскость L перпендикулярны.
- Плоскость F и плоскость L являются скрещивающимися.
+ Плоскость F и плоскость L параллельны.
- У плоскости F и плоскости L есть одна точка пересечения.
15. При условии, что прямые P и R параллельны третьей прямой Q,:
- прямая P будет перпендикулярна прямой R.
- прямая P и прямая R будут иметь одну точку пересечения.
- прямые P и R будут скрещивающимися.
+ прямые P и R будут параллельны между собой.
16. Есть две параллельные прямые и две параллельные плоскости. Между двумя данными плоскостями находятся отрезок XX1 и отрезок ZZ1 параллельных прямых. Выберите правильное утверждение:
- XX1 ║ ZZ1
+ XX1 = ZZ1
- XX1 // ZZ1
- XX1 и ZZ1 имеют точку пересечения
17. Сколько параллельных прямых можно провести через точку, находящуюся вне данной прямой?
+ одну
- две
- множество
- ноль
18. В каком варианте представлен ответ с ошибочным суждением?
- Две плоскости считаются параллельными, если каждая из них параллельна третьей плоскости.
- Две параллельные линии могут образоваться в результате пересечения двух параллельных плоскостей третьей плоскостью.
+ Две пересекающиеся прямые, находящиеся в одной плоскости, называются параллельными.
- Отрезки двух параллельных прямых, заключенные между двумя параллельными плоскостями, всегда равны друг другу.
19. Дана трапеция ABCD, основа CD которой лежит в плоскости α. KN – средняя линия трапеции. Выберите вариант ответа, в котором указано правильное суждение:
- KN находится в плоскости α.
+ KN параллельна плоскости α.
- KN перпендикулярна плоскости α.
-KN параллельна AD.
тест-20. Точка N находится вне данной плоскости. Можно ли через нее провести плоскость, параллельную данной? Если да, то сколько?
+ можно, одну
- нельзя
- можно, две
- можно, множество
21. Выберите вариант ответа, в котором представлено правильное продолжение следующего утверждения: «Если S – это середина стороны AB треугольника ABC, сторона AC которого находится в плоскости α, то ...»:
- через точку S можно провести две прямые, которые будут параллельны плоскости α.
- прямая SC и плоскость α перпендикулярны.
+ через точку S можно провести лишь одну параллельную плоскости α плоскость.
- через точку S нельзя провести прямую, которая будет перпендикулярна плоскости α.
22. Прямая H лежит вне плоскости a и является параллельной с прямой J, которая находится в данной плоскости. Выберите ошибочное суждение:
- Прямая H и прямая J не пересекаются.
+ Прямая H и прямая J перпендикулярны.
- Прямая J и плоскость a параллельны.
- Прямая H параллельна плоскости a.
23. Выберите ошибочное утверждение:
+ У прямой и плоскости может быть лишь одна общая точка.
- Две параллельные плоскости никогда не будут пересекаться.
- В одной плоскости могут лежать любые пять точек.
- В одной плоскости могут находиться две параллельные прямые.
24. Прямая M и плоскость α не имеют ни одну общую точку. Это значит, что:
- прямая M пересекается с другой прямой, лежащей в плоскости α.
- прямая M и плоскость α пересекаются.
- в плоскости α лежит прямая M.
+ плоскость α и прямая M параллельны.
25. Что является пересечением двух плоскостей в пространстве?
- точка
+ прямая
- окружность
- отрезок
26. Выберите вариант ответа, в котором неправильно указано продолжение следующей фразы: «Плоскость α и β являются параллельными между собой. Прямая K не лежит в плоскости α»:
+ Прямая K и плоскость β имеют одну общую точку пересечения.
- Прямая K лежит в плоскости β.
- Прямая K и плоскость β являются параллельными.
- Прямая K и плоскость α являются параллельными.
27. Какими могут быть две плоскости в пространстве?
- только пересекающимися
- только параллельными
- пересекающимися или скрещивающимися
+ параллельными или пересекающимися
28. Плоскость β пересекается с плоскостью α. Выберите правильное утверждение:
- Плоскость β перпендикулярна линии пересечения плоскостей α и β.
- Плоскость α является перпендикулярной линии пересечения плоскостей α и β.
- Плоскость β и плоскость α являются параллельными.
+ Одна из этих плоскостей параллельна линию пересечения плоскостей α и β.
29. Выберите вариант ответа, в котором указано неправильное продолжение следующей фразы: «Боковые стороны треугольника ABC параллельны плоскости β. Значит, ...»:
+ основание треугольника и плоскость β пересекаются.
- плоскость треугольника и плоскость β параллельны.
- основание треугольника и плоскость β являются параллельными.
- основание треугольника и плоскость β не пересекаются.
тест_30. Посмотрите на рисунок и скажите, сколько параллельных плоскостей можно провести через две прямые?
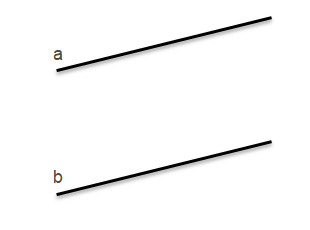
- одну
+ две
- три
- нельзя провести плоскостей
