Тесты по геометрии 10 класс. Тема: "Аксиомы стереометрии"
Правильный вариант ответа отмечен знаком +
1. Сколько всего аксиом стереометрии?
А. 5 –
Б. 7 –
В. 10 –
Г. 3 +
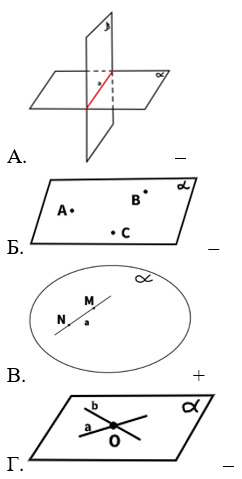
2. Какой из рисунков НЕ соответствует аксиомам стереометрии?
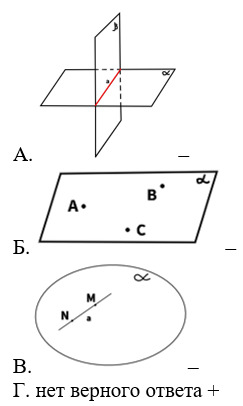
3. Выберите рисунок, соответствующий третьей аксиоме.
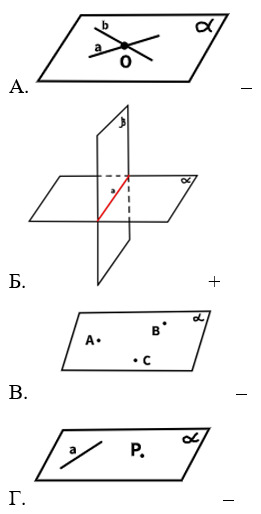
4. Какая из приведенных фигур НЕ является основной фигурой стереометрии?
А. плоскость –
Б. точка –
В. прямая –
Г. квадрат +
5. Укажите вторую аксиому стереометрии.
А. Через две пересекающиеся прямые проходит плоскость, и притом только одна. –
Б. Через прямую и не лежащую на ней точку проходит плоскость, и притом только одна. –
В. Если две точки прямой лежат в плоскости, то все точки прямой лежат в этой плоскости. +
Г. Если две плоскости имеют общую точку, то они имеют общую прямую, на которой лежат все общие точки этих плоскостей. –
6. Выберите рисунок, соответствующий первой аксиоме.
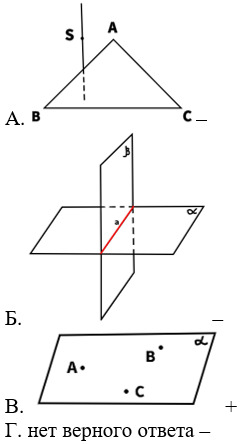
7. Выберите верную формулировку следствия из аксиом стереометрии.
А. Через несколько пересекающихся прямых проходит плоскость, и притом только одна. –
Б. Если три точки прямой лежат в плоскости, то все точки прямой лежат в этой плоскости. –
В. Через прямую и лежащую на ней точку проходит плоскость, и притом только одна. –
Г. Через две пересекающиеся прямые проходит плоскость, и притом только одна. +
8. Укажите первую аксиому стереометрии.
А. Через любые три точки, не лежащие на одной прямой, проходит плоскость, и притом только одна. +
Б. Если две точки прямой лежат в плоскости, то все точки прямой лежат в этой плоскости. –
В. Если две плоскости имеют общую точку, то они имеют общую прямую, на которой лежат все общие точки этих плоскостей. –
Г. Через две пересекающиеся прямые проходит плоскость, и притом только одна. –
9. Укажите третью аксиому стереометрии.
А. Через прямую и не лежащую на ней точку проходит плоскость, и притом только одна. –
Б. Если две плоскости имеют общую точку, то они имеют общую прямую, на которой лежат все общие точки этих плоскостей. +
В. Если две точки прямой лежат в плоскости, то все точки прямой лежат в этой плоскости. –
Г. Через две пересекающиеся прямые проходит плоскость, и притом только одна. –
тест 10. Какой аксиоме соответствует рисунок?
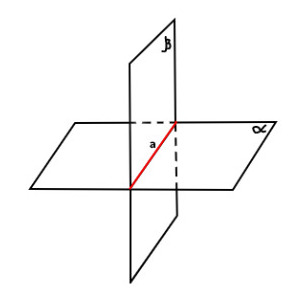
А. Первой –
Б. Второй –
В. Третьей +
Г. Никакой –
11. Выберете рисунок, соответствующий второй аксиоме.
12. Если две плоскости имеют общую точку, то они имеют общую прямую, на которой лежат все общие точки этих плоскостей. В таком случае говорят, что плоскости:
А. скрещиваются по прямой–
Б. пересекаются по прямой +
В. параллельны –
Г. равны –
13. Две плоскости НЕ могут иметь:
А. общую прямую –
Б. три точки, не лежащие на одной прямой +
В. общую точку –
Г. нет верного ответа –
14. Точки M, N, P лежат на одной прямой, точка K не лежит на ней. Через каждые три точки проводят плоскость. Сколько плоскостей получилось?
А. 4 –
Б. 12 –
В. 1 +
Г. ни одной –
15. В какой из указанных плоскостей лежит прямая AAı?
А. ABC –
Б. AAıB +
В. ABıCı –
Г. AıBıCı –
16. Точка P НЕ принадлежит плоскости:
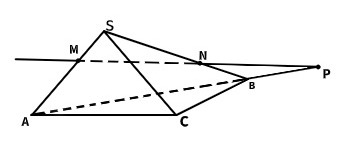
А. SAC +
Б. нет верного ответа –
В. SAB –
Г. ABC –
17. Каким плоскостям принадлежит точка N?
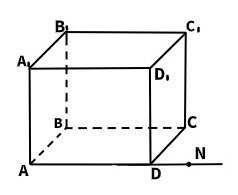
А. ABCD, AAıDıD +
Б. ABCD, AAıBıB –
В. AıBıCıDı, ABCD –
Г. BBıCıC, AAıDıD –
18. Назовите прямую, по которой пересекаются плоскости AıBıCı и CıBıB.
А. AıBı –
Б. CıC –
В. CıBı +
Г. AıCı –
19. Точка E НЕ принадлежит плоскостям:
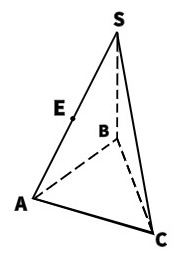
А. SAB, ABC –
Б. SBC, ABC +
В. SBC, SAC –
Г. SAC, ABC –
тест-20. Плоскости ABC принадлежит прямая:
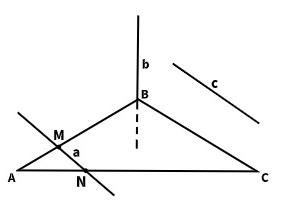
А. a +
Б. b –
В. c –
Г. ни одна –
21. Точки K, L, M, N не лежат в одной плоскости. Могут ли прямые KL и MN пересекаться? Могут ли какие-то три из них лежать на одной прямой?
А. да, нет –
Б. нет, да +
В. нет, нет –
Г. да, да –
22. Назовите прямую, по которой пересекаются плоскости NFB и FOB.
А. ON –
Б. OF –
В. FB +
Г. NB –
23. Каким плоскостям принадлежит точка S?
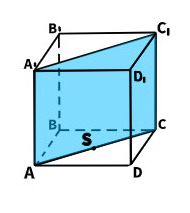
А. ABCD, AıBıCıDı –
Б. AAıBıB, AAıCıC –
В. ABCD, DDıCıC –
Г. AAıCıC, ABCD +
24. Выберите рисунок, на котором точка S принадлежит плоскости ABC.
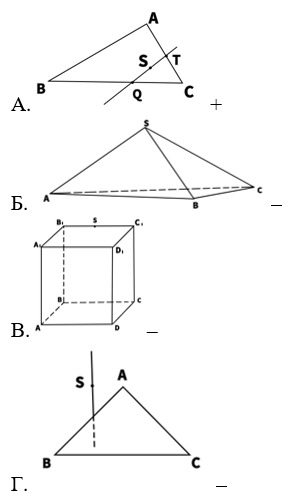
25. Верны ли следующие суждения?
а. Прямая, проходящая через вершину треугольника, всегда принадлежит плоскости этого треугольника.
б. Через две скрещивающиеся прямые проходит плоскость, и притом только одна.
А. верно только а –
Б. верно только б –
В. оба суждения верны –
Г. оба суждения неверны +
26. Верны ли следующие суждения?
а. Если одна точка прямой лежит в плоскости, то все точки прямой лежат в этой плоскости.
б. Через любые три точки проходит плоскость, и притом только одна.
А. верно только а –
Б. верно только б –
В. оба суждения верны –
Г. оба суждения неверны +
27. Верны ли следующие суждения?
а. Согласно первой аксиоме, через любые три точки, не лежащие на одной прямой, проходит плоскость, и притом только одна.
б. Через прямую и не лежащую на ней точку проходит плоскость, и притом только одна.
А. верно только а –
Б. верно только б –
В. оба суждения верны +
Г. оба суждения неверны –
28. Верны ли следующие суждения?
а. Существует лишь две аксиомы стереометрии.
б. Через три точки, лежащие на одной прямой, проходит плоскость, и притом лишь одна.
А. верно только а –
Б. верно только б –
В. оба суждения верны –
Г. оба суждения неверны +
29. Верны ли следующие суждения?
а. Если три точки окружности лежат в плоскости, то и вся окружность лежит в этой плоскости.
б. Если одна точка окружности лежит в плоскости, то и вся окружность лежит в этой плоскости.
А. верно только а +
Б. верно только б –
В. оба суждения верны –
Г. оба суждения неверны –
тест_30. Верны ли следующие суждения?
а. Прямая лежит в плоскости данного треугольника, если проходит через одну из вершин треугольника.
б. Прямая лежит в плоскости данного треугольника, если пересекает две стороны треугольника.
А. верно только а –
Б. верно только б +
В. оба суждения верны –
Г. оба суждения неверны –
