Тесты по геометрии 9 класс Сборник с ответами

Сборник тестовых вопросов по геометрии 9 класс

Правильный вариант ответа отмечен знаком +

1. На рисунке представлена формула. Что можно найти по ней?

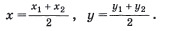
- это формула нахождения длины вектора;

- по данной формуле можно найти начало отрезка;

- это формула для вычисления конца отрезка;

+ по этой формуле можно с легкостью вычислить координаты середины вектора.

2. Чтобы найти «это», нужно взять первую координату вектора, возвести ее в квадрат. Затем вторую из координат вектора так же возвести в квадрат. Полученные значения сложить, а уже потом вычислить квадратный корень из имеющегося числа. Что нужно найти?

+ длину вектора;

- середину отрезка;

- начало вектора;

- конец вектора.

3. Чтобы узнать «эту вещь», нужно взять разность координат двух точек, возвести каждую из разностей в квадрат. После этого понадобится узнать число, полученное в результате сложения суммы квадратов. В конце потребуется вычисление квадратного корня. «Это» найдено. О чем идет речь?

- о нахождении длины отрезка;

- о формуле вычисления середины отрезка;

- о вычислении расстояния между началом и концом;

+ о расстоянии между двумя точками.

4. Требуется заполнить пустые строки в таблице. Внимание на рисунок.

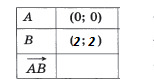
+ {2; 2};

- {-2; -2};

- {0; 2};

- {2; 0}.

5. Какое из приведенных уравнений можно отнести к уравнению окружности:

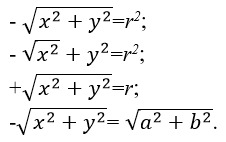
6. Дано уравнение окружности (x+4)²+(y-2)²=18 и точка К (5; 8). Нужно указать принадлежит ли точка данной окружности.

- точка лежит внутри окружности;

- точка лежит на окружности;

+ точка лежит вне окружности;

- нет верного ответа.

7. Что называется синусом угла λ из промежутка от 0°≤ λ ≤180°?

+ ордината точки;

- абсцисса точки;

- может быть, как абсцисса точки, так и ордината.

- верного ответа здесь нет.

8. Косинусом угла λ из промежутка от 0°≤ λ ≤180° является:

- это сложно сказать, требуется дополнительное построение;

- ордината точки;

+ абсцисса точки;

- и то, и другое.

9. Зная значение синуса и косинуса, можно ли вычислить тангенс угла? Если можно, то как это сделать?

- нельзя;

- можно, нужно найти отношение косинуса к синусу;

- можно, нужно взять половину косинуса;

+ можно, потребуется найти отношение синуса к косинусу.

тест 10. Среди представленных формул нужно выбрать основное тригонометрическое тождество.

+ sin² λ+cos² λ =1;

- sin³ λ+cos² λ =1;

- sin¹ λ+cos¹ λ =0;

- sin² λ=cos² λ.

11. На что нужно умножить половину произведения двух сторон треугольника при нахождении его площади?

+ на синус угла между ними;

- на синус любого угла треугольника;

- на косинус угла между ними;

- на косинус любого угла треугольника.

12. Чему пропорциональны стороны треугольника?

- косинусам противолежащих углов;

+ синусам противолежащих углов;

- тангенсам противолежащих углов;

- котангенсам противолежащих углов.

13. Какие из формулировок отражают содержание теоремы косинусов?

+ квадрат любой стороны треугольника равняется сумме квадратов двух остальных сторон минус удвоенное произведение этих сторон на косинус угла между ними;

- любая сторона треугольника равняется сумме квадратов двух остальных сторон минус удвоенное произведение этих сторон на косинус угла между ними;

- квадрат любой стороны треугольника равняется сумме квадратов двух других сторон минус произведение этих сторон на синус угла между ними;

- любая сторона треугольника равна сумме квадратов двух остальных сторон минус удвоенное произведение этих сторон на синус угла между ними.

14. Векторы, не равные нулю, перпендикулярны, когда:

- сумма всех координат векторов равняется нулю;

- сумма произведений всех абсцисс равна нулю;

- произведение всех ординат равно нулю;

+ сумма произведений абсцисс и ординат данных векторов равняется нулю.

15. Можно ли вписать в правильный многоугольник окружность или описать возле него её? Если да, то сколько?

+ можно только одну;

- можно только две;

- нельзя;

- ни одной окружности вписать нельзя.

16. Что можно найти по данной формуле C= 2πR?

- площадь круга;

- площадь кругового сектора;

- площадь правильного многоугольника;

+ длину дуги окружности.

17. Среди рисунков нужно выбрать тот, который изображает правильные многоугольники. Они выделены цветом.

18. При движении треугольник отображается на:

- любой треугольник;

- отрезок;

+ равный ему треугольник;

- квадрат.

тест-20. Сохраняются ли расстояния при параллельном переносе?

- этого нельзя сказать – нужны дополнительные построения;

- нет;

+да;

- здесь нет верного ответа.

21. Какая плоскость называется секущей?

+ плоскость, содержащая по обе стороны точки данного геометрического тела;

- плоскость, не имеющая точек данного тела;

- плоскость, проходящая мимо геометрического тела;

- нет верного ответа.

22. В прямоугольном параллелепипеде известны длина основания, равная 3, ширина, равняющаяся 4, а также его высота, имеющая длину 6. Чему будет равен его объём?

- 12;

- 48;

-18;

+72.

23. В пирамиде известна площадь основания. Она равна 8. Известна высота пирамиды. Ее длина 3. Выбрать верный вариант ответа, содержащий объем пирамиды.

- 24;

+ 8;

- 112;

- 72.

24. Имеется цилиндр с высотой 6. Площадь его основания равна 5. Чему равен его объём?

+30;

- 5;

- 15;

- 12.

25. В конусе известна высота. Она равняется 9. Известна площадь основания. Она равна 2. Объём этого конуса равен:

+6;

- 18;

- 3;

-9.

26. В шаре известен радиус. Его величина равна 4. Каков объем шара?

- 16;

- 18;

+64;

- 32.

27. Вращением какой фигуры вокруг оси можно получить цилиндр?

+ это прямоугольник;

- эта фигура треугольник;

- сфера;

- пятиугольник.

28. Чтобы получить конус, нужно вокруг его оси вращать эту фигуру. Указать ее среди представленных.

- сферу;

- ромб;

- прямоугольник;

+треугольник.

29. Вычислить площадь круга радиуса 6.

+ 36π;

- 6π;

- 18π;

-9π.

тест_30. На мишени имеются 4 кольца. Самое маленькое имеет радиус 1. Чему равна его длина?

- 1/2π;

- 1/3π;

- π;

+2π.

31. Среди приведенных формул нужно выбрать уравнение прямой в прямоугольной системе координат.

- r²x+ey=0;

- r³+et-1=0;

-y+t²=1;

+hx+ey+q=0.

32. Среди представленных окружностей требуется выбрать ту, что соответствует уравнению x²+y²=16.

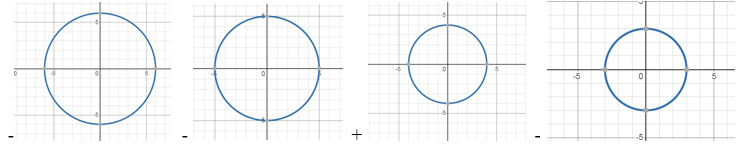
33. Нужно найти точки пересечения прямых x+2y-1=0 и 3x-2y+4=0. В приведенном решении указать этап с ошибкой.

Решение:

1) Составим систему уравнений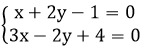 

2) Выразим x из первого уравнения системы:

x=1-2y

3) Подставим полученное выражение во второе уравнение:

3 (1-2y)-2y+4=0

3-6y-2y+4=0

-8y=-7

y=7/8

4) Теперь находим x:

x=1-2*7/8=-3/4

Верно ли выполнено решение? Если нет, то в каком из этапов допущена ошибка?

+ все верно;

- ошибка есть в первом этапе;

- имеется недочет на втором этапе решения;

- есть ошибка в третьем пункте.

34. Нужно продолжить лемму: если векторы коллинеарны, то…

- сумма одного из них с каким-то числом будет равняться второму вектору;

+существует такое число, что умножив на него второй вектор можно получить второй;

-существуют такие числа, при умножении на которые получаются рассматриваемые векторы;

-имеется такой вектор, при умножении на который можно получить любое число.

35. На сколько данных векторов можно разложить любой вектор на плоскости?

-на три;

-на четыре;

-на пять;

+на два.

36. Какие из пар векторов называются координатными векторами?

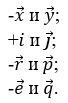
37. Каждая координата суммы нескольких векторов равна…

+сумме соответствующих координат данных векторов;

-произведению соответствующих координат этих самых векторов;

-разности координат данных векторов;

-поделенным друг на друга координатам этих самых векторов.

38. Координата разности нескольких векторов равна…

+разности координат соответствующих векторов;

-сумме разности координат соответствующих векторов;

-произведению сумм данных координат векторов;

-сумме произведений координат соответствующих векторов.

39. Если вектор умножается на какое-то число, то что произойдет с его координатами?

-ничего не произойдет;

-они увеличатся на это число;

+они умножаться на данное число;

- они уменьшатся на это число.

тест* 40. Каждая координата вектора равна…

+разности координат его начала и конца;

-сумме координат его начала и конца;

-произведению координат его начала и конца;

-ничему не равна.

41. Чему равна координата середины отрезка?

-ничему не равна;

+половине суммы соответствующих координат его концов;

-тройной сумме соответствующих координат концов данных отрезков;

-помноженным друг на друга координатам концов отрезков.

42. Чтобы вычислить длину вектора, нужно…

-сложить обе его координаты, а затем полученную сумму возвести в квадрат;

+каждую координату вектора требуется возвести в квадрат, полученные значения сложить, а затем извлечь квадратный корень;

-одну из координат возвести в квадрат;

-извлечь квадратный корень из суммы координат вектора.

43. Расстояние между двумя точками находится очень просто. Для этого…

+потребуется первая координата конца отрезка, из которой вычитается первая координата начала отрезка, затем это значение возводится в квадрат и тоже самое проделывается со второй парой координат, полученные значения складываются и из них извлекается квадратный корень;

-нужно будет сложить все пары координат между собой, затем возвести их в квадрат и извлечь из полученного значения квадратный корень;

-потребуется каждую координату вектора возвести в квадрат и сложить полученные значения;

-необходимо взять первую пару координат, сложить их и возвести в квадрат, затем тоже проделать со второй парой координат, из полученного значения извлечь квадратный корень.

44. Среди представленных уравнений нужно выбрать то, что является уравнением окружности.

- x²+2=0;

- y=2;

+ x²+y²=0;

- x³.

45. Имеется уравнение ax+by+c=0. Какое это уравнение?

+уравнение прямой;

-уравнение окружности;

-такого уравнения нет;

-уравнение параболы.

46. Требуется продолжить высказывание: Площадь треугольника равна половине…

-суммы некоторых сторон;

-суммы некоторых сторон, умноженных на синус угла между ними;

-произведения сторон, умноженных на косинус угла между ними;

+произведения двух из его сторон на синус угла между ними.

47. Стороны треугольника пропорциональны…

+синусам противолежащих углов;

-косинусам противолежащих углов;

-косинусам прилежащих углов;

-синусам прилежащих углов.

48. Чему равен квадрат стороны треугольника?

-он равняется сумме квадратов двух других сторон, перемноженных на синус угла между ними;

+он равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними;

-он равняется сумме квадратов других сторон, умноженных на косинус угла между ними;

-он равен сумме квадратов двух других сторон.

49. Скалярным произведением векторов называется…

+произведение их длин на косинус угла между ними;

-умножение координат вектора на синус угла между ними;

-поделенное значение длины вектора на косинус угла между ними;

-произведение их длин на синус угла между ними.

тест№ 50. Сколько окружностей можно описать около любого правильного многоугольника?

-три;

-четыре;

-две;

+одну.

51. Можно ли в правильный многоугольник вписать окружность?

+да;

-нет;

-при особых обстоятельствах;

-нужно посмотреть на рисунок.

52. Что общего у вписанной в правильный многоугольник окружности и описанной около него окружности?

-ничего;

-стороны;

+центр;

-радиус.

53. Как можно вычислить площадь правильного многоугольника?

+для этого нужно знать половину радиуса вписанной в него окружности, умноженной на периметр;

-потребуется знать радиус вписанной в него окружности, помноженной на периметр;

-нужно будет знать радиус описанной вокруг него окружности, умноженной на радиус вписанной окружности;

-потребуется знать радиус описанной вокруг него окружности, умноженной на радиус половину периметра.

54. На каком из рисунков представлен цилиндр?

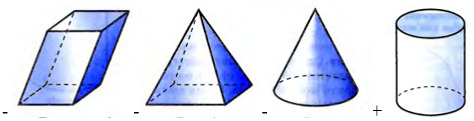
55. Какой из рисунков иллюстрирует конус?

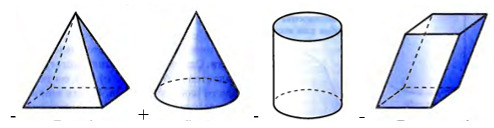
56. На котором рисунке имеется пирамида?

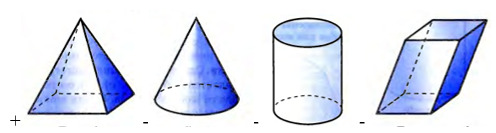
57. Чтобы найти объем куба нужно…

-возвести в квадрат одну из его сторон;

+возвести в куб одну из его сторон;

-извлечь квадратный корень из одной из его сторон;

-одна из его сторон и будет объемом.

58. Для того, чтобы вычислить объем параллелепипеда следует…

-знать площадь основания и этого достаточно;

-знать ее высоту;

+знать площадь основания, умноженного на высоту;

-знать половину основания.

59. Чтобы найти объем пирамиды, нужно…

+умножить треть площади основания на высоту;

-умножить половину площади основания на высоту;

-умножить площадь основания на высоту;

-умножить площадь на площадь боковой поверхности.

тест" 60. Для того, чтобы найти объем шара, нужно…

-умножить число пи на радиус;

+перемножить число пи и 4/3 радиуса;

-перемножить число пи и ½ радиуса;

-перемножить число пи и 5 радиусов.

61. Что является основанием конуса?

-квадрат;

+круг;

-прямоугольник;

-треугольник.

62. Основанием параллелепипеда является…

-квадрат;

-круг;

+прямоугольник;

-треугольник.

63. Что является основанием куба?

+квадрат;

-круг;

-прямоугольник;

-треугольник.