Тесты по геометрии 9 класс. Тема: "Простейшие задачи в координатах"
Правильный вариант ответа отмечен знаком +
1. Верно ли то, что у равных векторов равные координаты?
- нет;
+да;
- не знаю;
- сложно сказать.
2. Векторы, которые по своему направлению совпадают с осями координат, а также имеют длину, равняющуюся единице, называются следующим образом:
- единственные векторы;
- коллинеарные векторы;
- противоположно направленные векторы;
+ координатные векторы.
3. Что есть единичные векторы?
+ их длина равна единице;
- они единственные;
- это равные векторы;
- это векторы, координаты которых помножены на определенное число.
4. Этот подход к исследованию особенностей геометрических фигур, при помощи уравнений и неравенств, позволяет применять в геометрии алгебраические методы. При нем вводится система координат. Как называется данный метод?
+ метод координат;
- подход Бернулли;
- метод алгебры;
- геометрический подход.
5. При нахождении чего требуется вычислить половину суммы координат концов отрезка?
- при вычислении начала отрезка;
- при нахождении длины отрезка;
+ при поиске середины отрезка;
- при вычислении расстояний между двумя точками.
6. Для того, чтобы найти длину вектора, требуется сделать следующее:
+ возвести первую его координату в квадрат, затем вторую координату, полученные значения сложить и извлечь из конечного результата квадратный корень;
- возвести абсциссу и ординату вектора в квадрат, затем из большего значения вычесть меньшее, извлечь квадратный корень;
- из абсциссы и ординаты извлечь квадратный корень, затем полученные значения сложить;
- сложить координаты вектора, возвести в квадрат, затем извлечь квадратный корень.
7. В треугольнике даны две точки с координатами. Они соединены отрезком. Требуется найти длину этого отрезка. Это можно сделать следующим способом:
+ нужно из координат конца отрезка вычесть координаты начала отрезка, затем возвести в квадрат, по отдельности, полученные значения абсцисс и найденные значения ординат, найти их сумму и извлечь квадратный корень;
- потребуется вычесть из координат конца отрезка начало, затем возвести получившееся значение в квадрат;
- нужно возвести все координаты в квадрат, сложить их и извлечь квадратный корень;
-понадобится вычесть значения вторых координат из первых, затем сложить их и извлечь квадратный корень.
8. Имеется таблица. Нужно выяснить чему равен x.
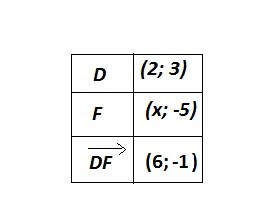
-1,5;
- 14;
-8;
+10.
9. Требуется указать верное значение на месте пустого пространства в таблице.
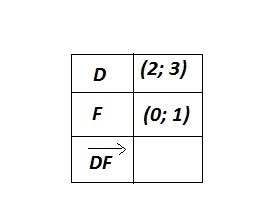
- (1; 2);
- (-1; -2);
- {-1; 2};
+{1; 2}.
тест 10. Дан вектор с координатами {4; 3}. Найти длину этого вектора.
+5;
- 1;
- 7;
- 3,5.
11. В треугольнике даны координаты двух вершин – S (4; 6), Q (-3; 6). Чему будет равна длина SQ?
- √12;
- 1;
-√21;
+7.
12. По рисунку определить координаты точек и найти длину GH.
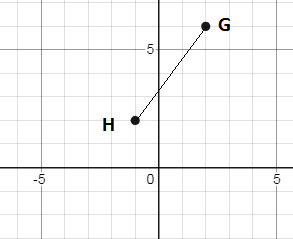
+5;
- 3;
-6;
- 8.
13. Дана задача и ее решение. Указать на каком этапе решения допущена ошибка.
Задача. Требуется найти расстояние между двумя точками D (5; 3) и J (4; 2).
Решение:
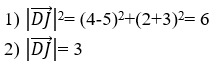
- 1;
- 2;
+ 1, 2;
- всё верно.
14. Дан четырехугольник с прямыми углами. Нужно доказать, что произвольная точка делит поровну его диагонали. При решении этой задачи метод координат поможет следующим образом:
+ нужно будет построить систему координат, задать координаты вершин прямоугольника, найти и сравнить длины отрезков, соединяющих вершины прямоугольника с данной точкой;
- потребуется взять линейку сделать соответствующие измерения;
- понадобится построить систему координат и всё сразу станет понятно;
- потребуется построить систему координат, задать координаты вершин прямоугольника и сравнить длины диагоналей между собой.
15. Каким образом можно узнать координаты определенного вектора?
- нужно заглянуть в тетрадь и всё сразу станет понятно;
- координаты вектора можно найти поделив пополам координаты его начала и конца;
- координаты вектора равны половине произведения его начала и конца;
+ координаты вектора равны разности координат его начала и конца.
16. Дан рисунок. Нужно найти по нему координаты точки A.
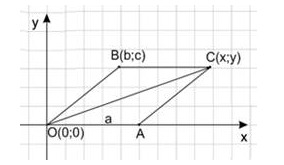
+(a; 0);
-(0; a);
-(b; c);
-(a; a).
17. На рисунке изображен параллелограмм. Какие координаты имеет точка C? Выбрать верное умозаключение.
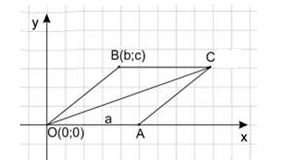
- на рисунке параллелограмм, а в нем противолежащие углы равны, поэтому C(0; 0);
+OABC – параллелограмм, следовательно, OA=BC=a, точка С имеет ординату с, так как расположена на прямой y=c. Поэтому, по формуле нахождения расстояния, между двумя точками находим, что абсцисса точки C равна a+b;
- обе координаты C равны координатам B, так они лежат на одной прямой, поэтому C(b; c);
- OABC – параллелограмм, а это значит, что BC=OA=a. Поэтому координаты точки C нужно найти по формуле нахождения расстояния между точками С (a; c).
18. Указать задачу для решения которой можно применить метод координат.
- доказать, что четырёхугольник – прямоугольник. Найти его площадь, если даны координаты вершин;
+ требуется доказать, что сумма квадратов всех сторон параллелограмма равна сумме квадратов его диагоналей;
- найти координаты медианы треугольника, если известны координаты его вершин;
- найти длину вектора с координатами {1; 2}.
19. Среди представленных формул выбрать ту, по которой можно вычислить длину вектора.
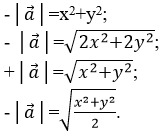
тест-20. Требуется выбрать среди формул ту, которая подходит для нахождения расстояния между двумя точками.
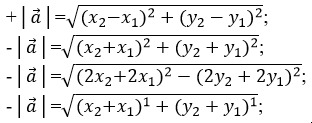
21. Которая из формул подойдет для вычисления середины отрезка.
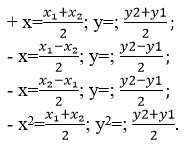
22. Какая из представленных формул наиболее подходящая для нахождения векторных координат.
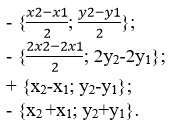
23. Вершина Z треугольника лежит на положительной полуоси абсцисс. Расстояние от начала координат до нее равно 4. Другая вершина треугольника H лежит на отрицательной полуоси ординат. Длина до неё равна 5. Каковы координаты этих вершин?
- Z(0;4), H(-5; 0);
- Z(4;-5), H(0;-5);
- Z(-5;4), H(4;-5);
+ Z(4;0), H(0; -5).
24. Известна длина вектора 4 и его абсцисса 3. Чему равна ордината вектора?
- 7;
- 4;
- 2√7;
+√7.
25. Координата суммы нескольких векторов равна:
+ сумме координат соответствующих векторов;
- разности координат одного из векторов;
- произведению координат каждого из векторов;
- сумме разностей координат каждого из векторов.
26. Координата разности двух и более векторов равняется:
- разности координат векторов, заключенных в квадрат;
+разности координат данных векторов;
- произведению всех координат векторов;
- делению каждой координаты вектора на другую его координату.
27. Координата произведения вектора на определенное число равна:
+ произведению координат данного вектора на определенное число;
- сумме координат, перемноженных между собой;
- разности координат векторов, умноженных на определенное число;
- перемноженному значению каждой координаты на другую.
28. Даны два вектора ![]() Найти координаты середины отрезка.
Найти координаты середины отрезка.
- (2; 3);
- (3/2; ½);
+ (1/2;3/2);
- (1; 2).
29. Имеется координата середины отрезка D(3; 2) и вектор ![]() . Найти второй вектор.
. Найти второй вектор.
-{1; 3};
-{-2; -3};
+{2; - 3};
-{0; 3}.
тест_30. Можно ли узнать координаты второго вектора, если даны координаты середины отрезка и один из векторов?
+ можно;
- нельзя;
- нужно построить систему координат;
- это зависит от варианта построения.
