Тесты по геометрии 7 класс. Тема: "Сумма углов треугольника"
Правильный вариант ответа отмечен знаком +
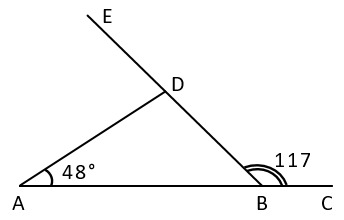
1. На рисунке представлен ΔABD, ∠CBD является внешним для этого треугольника, ∠CBD=117°. Вычислите, чему равен угол ADE.
1) 48° -
2) 69° -
3) 111° +
4) 165° -
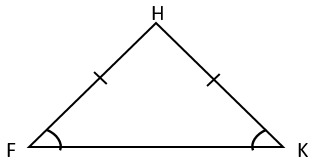
2. Треугольник FHK – равнобедренный. Известно, что угол HKF равен 54°. Найдите, чему равен угол при вершине H.
1) 54° -
2) 72° +
3) 108° -
4) 120° -
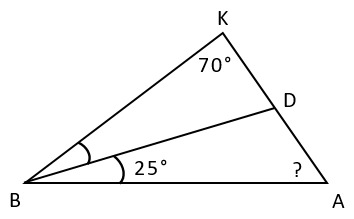
3. DB – биссектриса треугольника ABK, ∠AKB=70°, ∠ABD=25°. Градусная мера угла KAB равна:
1) 40° -
2) 50° -
3) 60° +
4) 70° -
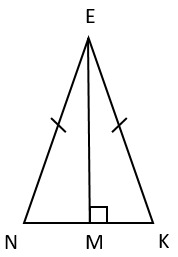
4. В равнобедренном треугольнике NEK проведена высота ME. Вычислите градусную меру угла при основании ENK, зная, что ∠KEN=44°.
1) 44° -
2) 45° -
3) 68° +
4) 90° -
5. На рисунке представлен произвольный треугольник KNB, угол ABK для которого является внешним. Каким образом можно вычислить градусную меру данного угла?
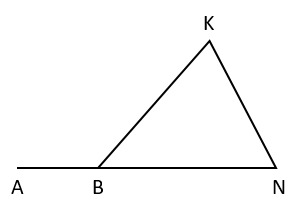
1) ∠KBN+∠KNB -
2) ∠ABN-∠KNA -
3) ∠BKA+∠BKN -
4) ∠NKB+∠BNK +
6. Выберите вариант ответа, в котором перечислены углы существующего треугольника:
1) 45°, 45°, 45° -
2) 40°, 50°, 60° -
3) 50°, 60°, 70° +
4) 5°, 125°, 45° -
7. Параллельно одной из сторон треугольника FHB проведена прямая AP. ∠BFH=50°, ∠PHB=65°. Вычислите градусную меру ∠BHF.
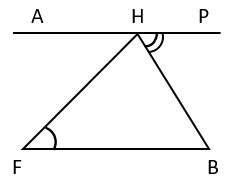
1) 45° -
2) 50° -
3) 60° -
4) 65° +
8. Параллельно основанию треугольника проведена параллельная прямая. Найдите величину неизвестного угла.
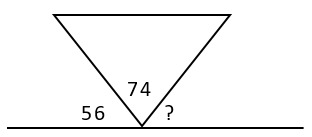
1) 50° +
2) 56° -
3) 60° -
4) 74° -
9. Треугольник DBN является произвольным, ∠BDN=75°, ∠NBD=50°. Найдите величину оставшегося неизвестным угла треугольника.
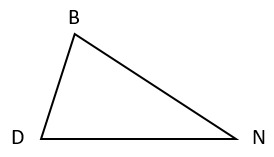
1) 50° -
2) 55° +
3) 60° -
4) 75° -
тест 10. На рисунке представлена информация о треугольниках, найдите с её помощью величину угла MAH.
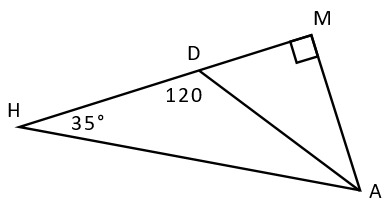
1) 50° -
2) 55° +
3) 60° -
4) 65° -
11. В прямоугольном треугольнике ABC известны длины гипотенузы и одного из катетов. Чему равна градусная мера угла ACB?
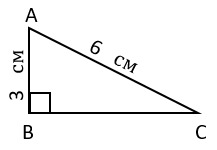
1) 30° +
2) 45° -
3) 60° -
4) 90° -
12. В треугольнике KAB проведена биссектриса AD, ∠BDA=100°, ∠ABD=45°. Вычислите градусную меру угла BKA.
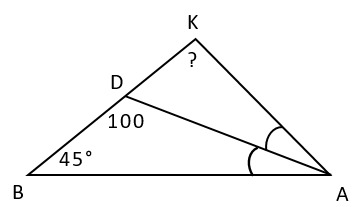
1) 45° -
2) 50° -
3) 60° -
4) 65° +
13. После продления сторон CB и AC в треугольнике BCA образовались внешние углы, величинами 80 и 130 градусов. Найдите градусную меру угла BCA.
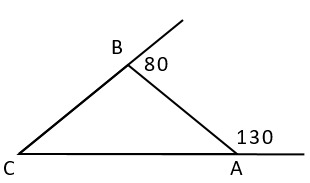
1) 30° +
2) 45° -
3) 60° -
4) 90° -
14. На рисунке представлены треугольники KPA и DPE так, что AK||DE. Исходя из известных градусных мер, вычислите величину угла EPD.
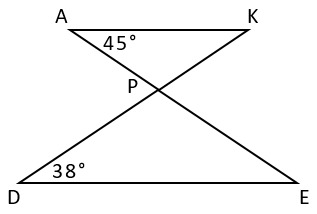
1) 76° -
2) 83° -
3) 97° +
4) 142° -
15. Какова градусная мера угла при основании равнобедренного прямоугольного треугольника?
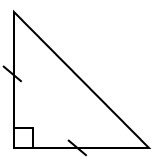
1) 30° -
2) 45° +
3) 60° -
4) 90° -
16. Выберите вариант ответа. Реальный треугольник может включать в себя:
1) два тупых угла -
2) тупой и прямой угол -
3) три острых угла +
4) пара прямых углов -
17. На рисунке изображён равнобедренный треугольник. Какова градусная мера неизвестного угла?
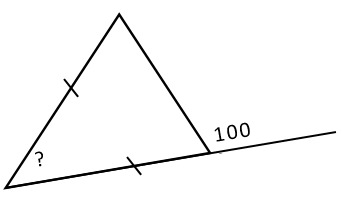
1) 30° -
2) 45° +
3) 60° -
4) 90° -
18. Вычислите градусную меру угла прямоугольного треугольника, при условии, что величина второго угла 55°.
1) 35° +
2) 45° -
3) 90° -
4) 125° -
19. С помощью изображения треугольника KNB найдите градусную меру угла K.
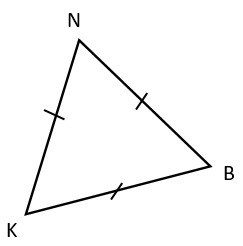
1) 45° -
2) 60° +
3) 90° -
4) 120° -
тест-20. Величины углов треугольника NAT имеют следующие отношения: ∠N:∠A:∠T=4:8:6. Градусная мера угла A:
1) 23° -
2) 48° -
3) 80° +
4) 180° -
21. В треугольнике PMA проведена пара биссектрис – LA и PB. Определите величину угла их пересечения ∠AOP, если ∠MPA=70°, ∠PAM=78°.
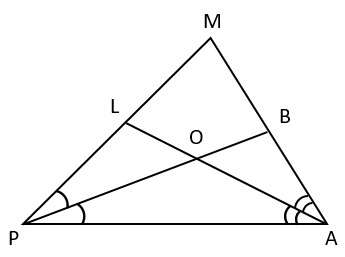
1) 74° -
2) 90° -
3) 106° +
4) 120° -
22. Треугольник BKC – равнобедренный, BK=KC. Найдите величину угла C.
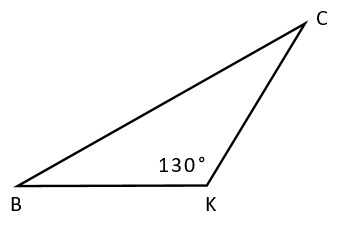
1) 25° +
2) 30° -
3) 50° -
4) 65° -
