Тесты - Логарифмические уравнения 11 класс с ответами

Тесты по алгебре 11 класс. Тема: "Логарифмические уравнения"

Правильный вариант ответа отмечен знаком +

1. Как выглядит простейшее логарифмическое уравнение?

a. log_ax = b +

b. log_aa = 1 -

c. 3log = b -

d. log_bx = a -

2. log₃1/9 = …

a. 27 -

b. 2 -

c. 12 -

d. -2 +

3. Чему равен x в уравнении log₄x = 3?

a. 12 -

b. 64 +

c. 7 -

d. 81 -

4. Что такое логарифмическое уравнение?

a. это уравнение, в котором неизвестные переменные находятся вне логарифмов -

b. это уравнение, в котором отсутствуют неизвестные переменные -

c. это уравнение, в котором неизвестные переменные находятся внутри логарифмов +

d. это уравнение, в котором неизвестные переменные представлены в виде логарифмов -

5. Из-за какого значения уравнение 1 + 2x = log₂(3x + 1) нельзя назвать логарифмическим?

a. 1 -

b. 2x +

c. 3x + 1 -

d. log₂ -

6. log₃x = … при x = ⅓

a. -1 +

b. 3 -

c. 1 -

d. 1/9 -

7. Действие, которое является обратным логарифмированию по некоторому основанию, - это …

a. аддитивность -

b. потенцирование +

c. инвариант -

d. тривиальность -

8. Чему равна область определения функции y=log_ax при a > 0, a≠1?

a. x > 0 +

b. x < 0 -

c. x = 0 -

d. x ⩽ 0 -

9. Какой математик является одним из изобретателей логарифмов?

a. Исаак Ньютон -

b. Джон Непер +

c. Андрей Колмогоров -

d. Леонтий Магницкий -

тест 10. График какого логарифма изображен на картинке?

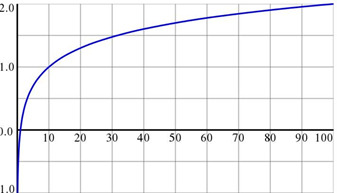
a. натурального -

b. десятичного +

c. двоичного -

d. логарифма числа b по основанию a -

11. Между какими числами установлено равенство в уравнении log_ab=c?

a. a и b -

b. a и c -

c. a, b и c +

d. b и c -

12. Чему равен x в уравнении log₂x = 3?

a. 9 -

b. 6 -

c. 5 -

d. 8 +

13. Как расшифровывается Одз логарифма?

a. область допустимых значений логарифма +

b. общее действительное значение логарифма -

c. однозначность логарифма -

d. одинарное значение логарифма -

14. log2 x₂ + х = log₂(х + 9) при x = …

a. 6 -

b. 3 +

c. 10 -

d. 4 -

15. Логарифмическое неравенство – это неравенство вида log_ab(x) > log_ac(x),где а … 0, a ≠ 1

a. < -

b. = -

c. ≫ -

d. > +

16. Область значений логарифмической функции y = log_ax равна …

a. (-1; +♾) -

b. (-♾; +♾) +

c. (-♾; 1) -

d. -1; 0) -

17. Чему равен логарифм произведения положительных сомножителей?

a. сумме логарифмов этих сомножителей +

b. разности логарифмов этих сомножителей -

c. частному логарифмов этих сомножителей -

d. произведению логарифмов этих сомножителей -

18. Как будет выглядеть уравнение log₃(2х-5) = log3х после применения потенцирования?

a. log_{2x - 1} = 2 -

b. log₃(2х-1) = 2 +

c. log₂(2х-1) = 2 -

d. log3(2х-1) = 2 -

19. Какого метода решения логарифмических уравнений не бывает?

a. применения основного логарифмического тождества -

b. метода введения новой переменной -

c. метода логарифмирования -

d. метода превращения логарифмов в десятичные дроби +

тест-20. В каких случаях можно убрать логарифмы из уравнения?

a. если в левой и правой частях уравнения одинаковые основания +

b. если в левой и правой частях уравнения разные степени -

c. если в левой и правой частях уравнения имеются одинаковые степени -

d. если в левой и правой частях уравнения разные основания -

21. Чему равен x в уравнении ?

a. 4 -

b. 3 +

c. 2 -

d. 7 -

22. Кем была изобретена логарифмическая линейка?

a. Эдмундом Гантером +

b. Вильгельмом Лейбницем -

c. Бернардом Риманом -

d. Пифагором -

23. log₅(x - 4) = 2 при x = …

a. 29 +

b. 16 -

c. 11 -

d. 7 -

24. Какое общее основание имеет уравнение log₈16 + log₈4 = 2?

a. 8 -

b. log₄ -

c. log -

d. log₈ +

25. log...125 = 3

a. 5 +

b. 8 -

c. 2 -

d. 9 -

26. Как будет выглядеть уравнение log²₄x - 2log₄x - 3 = 0 после введения новой переменной m?

a. m⁴ - 5 = 0 -

b. 2m + 3 = 0 -

c. m² - 2m - 3 = 0 +

d. 4m² - 2m = 3 -

27. Какой метод решения применим к уравнению log₃x = 2?

a. метод по определению логарифма +

b. метод подстановки -

c. метод потенцирования -

d. метод логарифмирования -

28. Из какой страны математик Джон Непер, автор работы «Описание удивительной таблицы логарифмов»?

a. Бельгия -

b. Шотландия +

c. Япония -

d. Англия -

29. Чему равен x в уравнении log₅x = 0?

a. 1 +

b. 0 -

c. 2 -

d. -1 -

тест_30. Какое из уравнений не решается методом логарифмирования?

a. 2x^{log2 x} = 32 -

b. log₂((2 + log₃(3 + x)) = 0 +

c.log^{log2 x} = 32 -

d. x^{lg x}= 10 -