Тесты - Тригонометрические уравнения 11 класс с ответами

Тесты по алгебре 11 класс. Тема: "Тригонометрические уравнения"

Правильный вариант ответа отмечен знаком +

1. Чему равен x в уравнении tg x = -√3?

a. -π/3 + πn, n ∈ ℤ +

b. π/3 - πn, n ∉ ℤ -

c. 3π - πn, n ∈ ℤ -

d. π + πn/3, n ∉ ℤ -

2. tg π/3 = …

a. √3/3 -

b. ½ -

c. -√2/2 -

d. √3 +

3. На что нужно заменить ctg x в выражении ctg x - 3tg x = 0, используя способ решения в виде сведения к одной функции?

a. 2tg x -

b. tg x / 2 -

c. 1/tg x +

d. tg x -

4. tg ½x = 12

a. x = arctg ½ - πn, n ∈ ℤ -

b. x = 2arctg12 + πn, n ∈ ℤ +

c. x = arctg6 + πn, n ∈ ℤ -

d. x = 12πn, n ∈ ℤ -

5. Какие задачи связаны с любой конкретной функцией?

a. прямая и обратная +

b. кривая и передняя -

c. линейная и противоположная -

d. направляющая и задняя -

6. В чем заключается решение множества тригонометрических функций?

a. в преобразовании в сложнейшие уравнения -

b. в сведении к простейшим уравнениям +

c. в обязательном использовании формулы приведения -

d. в изменении упорядоченного расположения чисел -

7. Чему равен x в уравнении cos x = 1?

a. π/2 - πn, n ∈ ℤ -

b. 2π + πn, n ∈ ℤ -

c. 2πn, n ∈ ℤ +

d. -π/2 + πn, n ∈ ℤ -

8. 

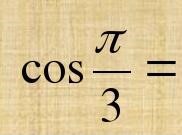
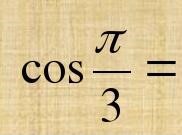
a. ½ +

b. 1 -

c. 0 -

d. ⅙ -

9. arcsin (-a) = …

a. arccos a -

b. -arcsin a +

c. arctg a -

d. -arcctg a -

тест 10. Какое тригонометрическое уравнение не имеет корней?

a. sin(4x² + 2x - 1) = -7 +

b. cos 2x = 0 -

c. cos x = -½ -

d. cos(2x - 3) = 0 -

11. Что является сложным аргументом в примере ctg(2x - π/3) = 1?

a. ctg -

b. 2x - π/3 +

c. 1 -

d. -π/3 -

12. Чему равен x в уравнении √3tg(3x - π/6) = 3?

a. π/6 + πn/3, n ∈ ℤ +

b. 3π - πn, n ∈ ℤ -

c. -π/2, n ∈ ℤ -

d. π/3 + 2πn, n ∈ ℤ -

13. При каком варианте уравнений x будет равен -π/2 + 2πn, n ∈ ℤ?

a. sin x = 0 -

b. sin x = 1 -

c. sin x = 2 -

d. sin x = -1 +

14. Каких тригонометрических уравнений не бывает?

a. однородных -

b. чужеродных +

c. неоднородных -

d. приводимых к квадратному относительно тригонометрической функции -

15. cos 2πn = …

a. 1 +

b. -1 -

c. ½ -

d. -⅙ -

16. Какая формула выражает тангенс половинного угла?

a. tg a/2 = sin a / 1 - cos a -

b. tg a/2 = 1 - cos a / sin a +

c. tg a/2 = 1 + sin a / cos a -

d. tg a/2 = cos a / sin a -

17. При каком значении a x = π/2 + 2πn, n ∈ ℤ в выражении sin x = a?

a. 1 +

b. 0 -

c. -1 -

d. ¼ -

18. cos 2x = … - sin²x

a. tg²x -

b. ctg²x -

c. 1/sin²x -

d. cos²x +

19. Какое из уравнений является тригонометрическим?

a. sin2x - x = 4 +

b. 1/4x - 0,11 = 0,14 -

c. 5x - 9 = 1 -

d. x - 2y = 7 -

тест-20. Какое обозначение не относится к тригонометрическим функциям?

a. tg -

b. ctg -

c. lg +

d. sin -

21. Сколько всего основных формул существует для решения тригонометрических уравнений?

a. 4 +

b. 2 -

c. 3 -

d. 1 -

22. sin2x = …

a. 2(sin x - cos x) -

b. sin2x + cos2x -

c. cos2x - sin2x -

d. 2sin x cos x +

23. Результаты каких выражений равны?

a. ctg π/6 и tg π/3 +

b. sin π/4 и cos π/6 -

c. tg π/4 и cos π/3 -

d. ctg π/3 и sin π/4 -

24. При каком значении x cos x = 1?

a. 2πn, n∈ ℤ +

b. πn, n ∈ ℤ -

c. π/3, ∈ ℤ -

d. π/6, n ∈ ℤ -

25. Дополнением какой науки ранее служила тригонометрия?

a. география -

b. химия -

c. астрономия +

d. геология -

26. Что относится к прикладным способам решения тригонометрических уравнений?

a. разложение на множители -

b. замена переменной -

c. однородные уравнения -

d. введение вспомогательного угла +

27. cos x = a, где |a| … 1

a. =-

b. ⩽ +

c. > -

d. ≈ -

28. cos x = 1

a. x = 2πn, n ∈ ℤ +

b. x = π/2 + πn, n ∈ ℤ -

c. x = π - πn, n ∈ ℤ -

d. x = -πn, n ∈ ℤ -

29. Какой метод не способствует нахождению корней тригонометрических уравнений?

a. алгебраический -

b. исторический +

c. геометрический -

d. арифметический -

тест_30. Как выглядит формула двойного угла cos2x?

a. cos²x - sin²x +

b. sin²x + cos²x -

c. 2sin x - 2cos x -

d. tg²x + ctg²x -