Тесты - Решение неравенств методом интервалов 9 класс с ответами

Тесты по алгебре 9 класс. Тема: "Решение неравенств методом интервалов"

Правильный вариант ответа отмечен знаком +

1. Методом интервалов называется:

+ алгоритм, включающий в себя нахождение нулей числителя и знаменателя, нанесение их на координатную ось абсцисс, определение знаков, полученных промежутков, и нахождение решения, соответствующего знаку исходного неравенства;

- алгоритм, включающий в себя нахождение нулей числителя, нанесение их на координатную ось абсцисс, определение знаков, полученных промежутков, и нахождение решения, соответствующего знаку исходного неравенства;

- алгоритм, включающий в себя нахождение нулей знаменателя, нанесение их на координатную ось абсцисс, определение знаков, полученных промежутков, и нахождение решения, соответствующего знаку исходного неравенства;

- алгоритм, включающий в себя нахождение нулей числителя и знаменателя, нанесение их на координатную ось ординат, определение знаков, полученных промежутков, и нахождение решения, соответствующего знаку исходного неравенства.

2. Альтернативным названием метода интервалов является:

- метод отрезков;

- графический метод;

- методом гаусса;

+ метод промежутков.

3. Если решением неравенства является один корень, а правая область имеет положительный знак по методу интервалов, то левая область:

- является нейтральной зоной;

+ имеет положительный знак;

- имеет отрицательный знак;

- является смешанной зоной.

4. При умножении обеих частей строгого неравенства на -1, знак неравенства:

- остается неизменным;

- меняется на противоположный знак, при этом само неравенство становится нестрогим;

+ меняется на противоположный знак;

- остается неизменным, при этом само неравенство становится нестрогим.

5. При нестрогом неравенстве нули знаменателя наносятся на координатную ось абсцисс:

- выколотыми точками, согласно знаку неравенства;

- закрашенными точками, согласно знаку неравенства;

+ выколотыми точками;

- не наносятся на координатную ось абсцисс.

6. Если в неравенстве множитель повторяется четное количество раз, то при переходе через найденный ноль знак в интервале на координатной оси:

- меняется при переходе через ноль;

+ остается неизменным;

- меняется на отрицательном участке оси;

- остается неизменным только на положительном участке оси.

7. Выполни первый шаг алгоритма решения неравенства методом интервалов (нахождение нулей функции)

- 0; 1; 4;

+ 0; -1; 4;

- 0; -1; -4;

- 0; 1; -4.

8. Выполни первый шаг алгоритма решения неравенства методом интервалов (нахождение нулей функции)

- -2; 0; -1; 4;

- 2; 1; -1; 4;

- -2; 0; -1; -4;

+ -2; 1; -1; 4.

9. Выполни первый шаг алгоритма решения неравенства методом интервалов (нахождение нулей функции) x - 3(x + 2x2) + 4 > 0:

- ⅓; -1;

+ ⅔; -1;

- ⅔; 1;

- ⅓; 1.

тест 10. Какое неравенство удовлетворяет графическому решению методом интервалов:

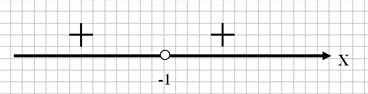
- x(x-4)>0;

+ x(x+2)+1>0;

- 3x<6;

- x≥2/(x-4).

11. Какое неравенство удовлетворяет графическому решению методом интервалов:

- x+1≤0;

- (x-4)(x+2)>0;

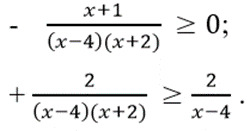
12. При решении какого неравенства будет наблюдаться участок без чередования знаков на интервалах:

- x+1≤0;

- (x-1)(x+2)>0;

+ |x+4|∙(2x-3)³∙(5-x)²≥0;

13. При решении какого неравенства будет наблюдаться участок c чередованием знаков на интервалах:

- 2(x²-6x)≤-9;

- (x-2)(x+2)>0;

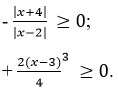
14. Решить неравенство (x-2)(x-4)>0:

+ (-∞;2)∪(4;+∞);

- (4;+∞);

- (-∞;2);

- (2;4).

15. Решить неравенство (x+3)(x-1)<0:

- (-∞;-3)∪(1;+∞);

+ (-3;1);

- (-∞;-3);

- (1;3).

16. Решить неравенство 2(x-2)≥3(x-4):

- (-∞;8);

- (8;+∞);

+ (-∞; 8];

- [8; +∞).

17. Решить неравенство x(5-x)(7+x)>0:

- (0;+∞);

- (0;5);

+ (-∞;-7)∪(0;8);

-(-7;0)∪(5;+∞).

18. Решить неравенство (x-6)(x-9)<0:

- (-∞;6)∪(9;+∞);

- (9;+∞);

- (-∞;6);

+ (6;9).

19. Решить неравенство (x+2)(x-7)>0:

+ (-∞;-2)∪(7;+∞);

- (-2;7);

- (-∞;-2);

- (2;7).

тест-20. Решить неравенство (x-3)≥(-x-9):

- (-∞;-3);

- (-3;+∞);

+ (-∞; -3];

- [-3; +∞).

21. Решить неравенство x(2-x)(1+x)<0:

- (-1;+∞);

- (0;2);

+ (-∞;-1)∪(0;2);

-(-1;0)∪(2;+∞).

22. Решить неравенство x(4-2x)(1+x)(x-3)<0, указав наибольший целый корень, который входит в диапазон решения:

+ +∞;

- 2;

- 3;

--∞.

23. Решить неравенство 3x(7x-21)(6-x)(x+25)>0, указав наибольший целый корень, который входит в диапазон решения:

- +∞;

+ 5;

- 6;

--∞.

24. Решить неравенство x(x-1)² (-x+2x-4)>0:

- (-∞;0);

- (0;4);

+ (-∞;0)∪(4;+∞);

-(4;+∞).

25. Решить неравенство x(x-1)² (-x+2x-4)≤0, указав наибольший целый корень, который входит в диапазон решения:

- 0;

- 3;

+ 4;

-2.

26. Решить неравенство x(x-1)² (x+1)²≥0, указав наибольший целый корень, который входит в диапазон решения:

+ +∞;

- 0;

- 1;

--1.

27. Решить неравенство x(x-1)² (x+1)²≤0, указав наибольший целый корень, который входит в диапазон решения:

- -∞;

- 0;

+ 1;

--1.

28. Решить неравенство (x-6)(x-9)<0, указав наименьший целый корень, который входит в диапазон решения:

6;

9;

- 0;

+ 7.

29. Решить неравенство (x+2)(x-7)≤0, указав наименьший целый корень, который входит в диапазон решения:

+ -2;

- 7;

- -1

- 0.

тест_30. Решить неравенство (x-3)≥(-x-9), указав наибольший целый корень, который входит в диапазон решения:

- -∞;

- 0;

+ -3;

- -2.