Тесты - Неравенства 9 класс с ответами

Тесты по алгебре 9 класс. Тема: "Неравенства"

Правильный вариант ответа отмечен знаком +

1. Какое выражение не является неравенством:

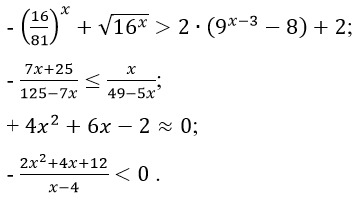
2. Какого вида неравенства не существует:

- линейное неравенство;

- квадратное неравенство;

- дробно рациональное неравенство;

+ параболическое неравенство.

3. Линейное неравенство выражено формулой:

+ ax>b;

- a^f(x) <a^g(x) ;

-ax²+bx+c≤0;

- f(x)/g(x) ≥0.

4. Чему не должно равняться число а в линейном неравенстве:

- a ≠ -∞;

+ a ≠ 0;

- a ≠ +∞;

- a ≠ 1.

5. Соотнести графическое решение линейного неравенства с формой записи ответа:

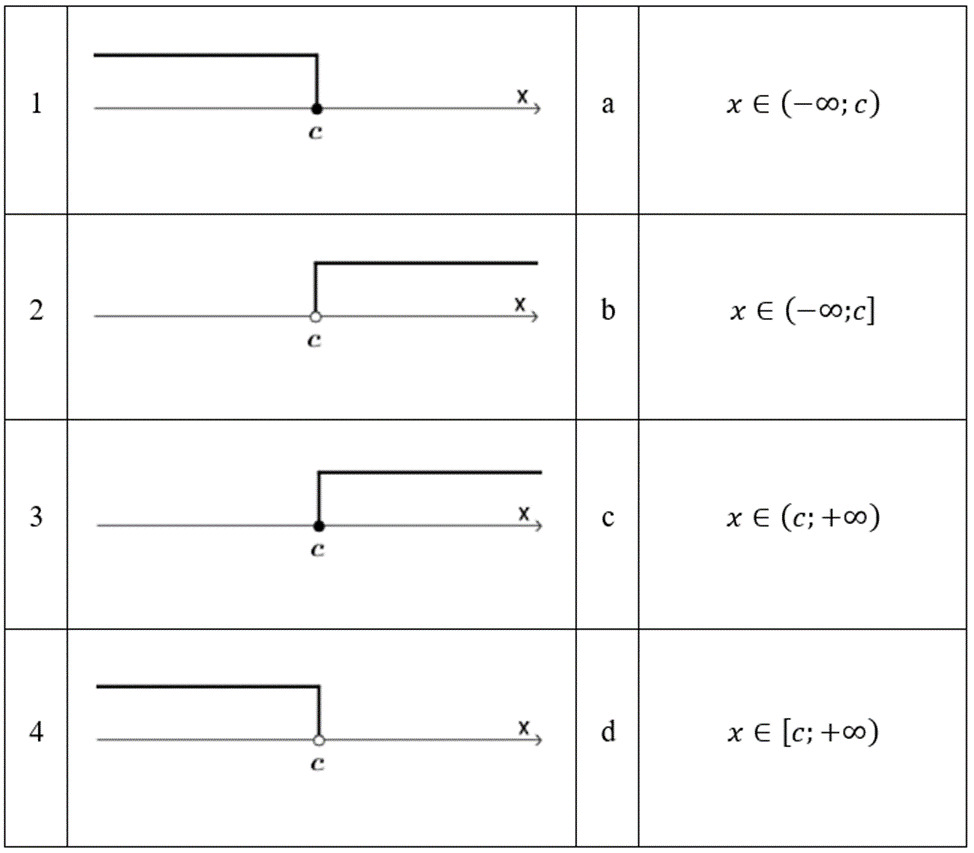
+ 1-b, 2-c, 3-d, 4-a;

- 1-a, 2-a, 3-d, 4-b;

-1-b, 2-d, 3-c, 4-a;

- 1-a, 2-d, 3-c, 4-b.

6. Решить линейное неравенство 3∙(2x+4)+x-4∙(x-5)≥18x-28

- x∈(-∞;4);

+ x∈(-∞;4];

- x∈[4;+∞);

- x∈(4;+∞).

7. Решить линейное неравенство 5x+2∙(x-4)+5∙(x-3)≥7x+7

- x∈(-∞;6);

- x∈(-∞;6];

+ x∈[6;+∞);

- x∈(6;+∞).

8. Решить линейное неравенство: 7x+3∙(2x-5)-x-2∙(4x+5)<6x+4∙(x-7)+9

- x∈(-∞;1);

- x∈(-∞;1];

- x∈[1;+∞);

+ x∈(1;+∞).

9. Решить линейное неравенство: 7-4x+2∙(x+7)-2x∙(2+2x)+3x²>6x-x²+9

+ x∈(-∞;1);

- x∈(-∞;1];

- x∈[1;+∞);

- x∈(1;+∞).

тест 10. Решить линейное неравенство: 9x-x²+2∙(0,5x-2)-x∙(4-x)≤6x+4

+ x∈(-∞;+∞);

- x∈(-∞;0];

- x∈[0;+∞);

- x∈0.

11. Решить линейное неравенство: 3x-2x²+4∙(0,25x-2)>2x²+4x+12

+ x∈(-∞;+∞);

- x∈(-∞;20];

- x∈[20;+∞);

- x∈∅.

12. Квадратное неравенство выражено формулой:

- ax>b;

- a^f(x) <a^g(x) ;

+ ax²+bx+c≤0;

- f(x)/g(x) ≥0.

13. Какой универсальный метод решения квадратных неравенств принят и существует:

- компьютерный анализ;

+ метод интервалов;

- нахождение области определения;

- функционально-графический метод.

14. Если решением неравенства является один корень, а правая область имеет положительный знак по методу интервалов, то вторая область имеет:

- нейтральная зона;

- положительный знак;

+ отрицательный знак;

- положительно-отрицательная зона.

15. Укажите неверную формулу нахождения корней квадратного неравенства:

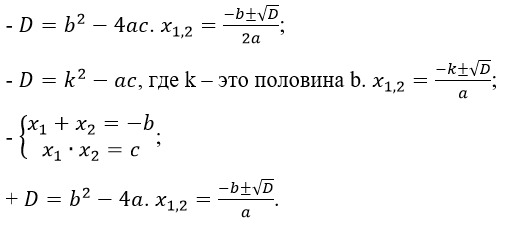
16. Интерпретировать графическое решение квадратного неравенства x∙(x-2)+0,5∙(12+4x)+x²-4>x+x²+14 в числовую запись ответа:

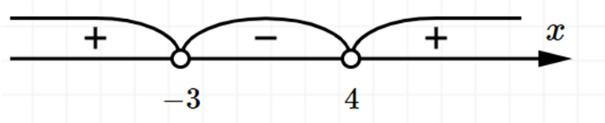
- x∈(-∞;-3);

+ x∈(-∞;-3)∪(4;+∞);

- x∈(4;+∞);

- x∈(-3;4).

17. Решить квадратное неравенство: 2-4x+2x∙(x-1)+x∙(3+x)+x²>3x-2x²+14

+ x∈(-∞;-1)∪(2;+∞);

- x∈(-∞;-1);

- x∈(2;+∞);

- x∈(-1;2).

18. Решить квадратное неравенство: 5-4x+0,25x∙(8x-4)+2x∙(2+x)-4x²+7≥4x+x²+14

- x∈(-2; -1);

- x∈[-2; -1);

+ x∈[-2; -1];

- x∈(-2;1).

19. Решить квадратное неравенство: 1-2x+2∙(3x+x² )-4x²+5<7x-x²+2

+ x∈(-∞;-4)∪(1;+∞);

- x∈(-∞;-4);

- x∈(1;+∞);

- x∈(-4;1).

тест-20. Решить квадратное неравенство: 1-x+2-2x²+5<-7x-3x²-1

- x∈(-∞;+∞);

- x=-3;

- x∈(-∞;-3)∪(-3;+∞);

+ x∈∅.

21. Дробно рациональное неравенство – это

+ неравенство, которое можно привести к дроби, знаменатель которой будет содержать искомую переменную;

- неравенство, которое можно привести к дроби, числитель которой будет содержать искомую переменную;

- неравенство, которое можно привести к дроби, числитель и знаменатель которой будут содержать искомую переменную;

- неравенство, в составе которого есть дробь.

22. Дробно рациональное неравенство выражено формулой:

- ax>b;

- a^f(x) <a^g(x) ;

-ax²+bx+c≤0;

+ f(x)/g(x) ≥0.

23. Какое неравенство не является дробно рациональным неравенством:

- (x-1)/(x+6)>0;

- (x²+3x-1)/(x+2)<0;

-3/(x-9)≤0;

+ (x-1)/2≥0.

24. При решении дробно рационального неравенства методом интервалов полученные нули знаменателя при нестрогом знаке неравенства (≤или ≥) на оси x отмечаются:

- положительные значения - жирными точками, а отрицательные значения – выколотыми точками;

- жирными точками, то есть значения входят в область решения;

+ выколотыми или пустыми точками, то есть значения не входят в решение неравенства;

- отрицательные значения – жирными точками, а положительные значения – жирными точками.

25. Решить дробно рациональное неравенство (x-1)/(x+2)≥0:

+ x∈(-∞;-2)∪[1;+∞);

- x∈(-∞;-2)∪(1;+∞);

- x∈(-2; 1];

- x∈(-2;1).

26. Решить дробно рациональное неравенство (3x-6)/(x+2)<0:

- x∈(-∞;-2)∪[2;+∞);

- x∈(-∞;-2)∪(2;+∞);

- x∈(-2; 2];

+ x∈(-2;2).

27. Показательное неравенство выражено формулой:

- ax>b;

+ a^f(x) <a^g(x) ;

-ax²+bx+c≤0;

- f(x)/g(x) ≥0.

28. При равных основаниях меньше единицы (0<a<1) при решении показательного неравенства знак неравенства:

+ меняется на противоположный;

- остается неизменным;

- становится нестрогим;

- становится строгим.

29. Привести к одному основанию неравенство 2^x>256 и найти x:

- 2^x>2⁸ =>x<8;

+ 2^x>2⁸ =>x>8;

- 2^x>2⁸ =>x≥8;

- 2^x>2⁸ =>x≤8.

тест_30. Решением показательного неравенства 49^{(x-2(1+x)+2x)}>7^(2x+1) является:

+ x∈(-∞;-1);

- x∈(-∞;-1];

- x∈(-1;+∞);

- x∈(-1;+∞).