Тесты - Геометрическая прогрессия 9 класс с ответами

Тесты по алгебре 9 класс. Тема: "Геометрическая прогрессия"

Правильный вариант ответа отмечен знаком +

1. Геометрическая прогрессия – это

- последовательность b_n, в которой каждый предыдущий член можно найти, если последующий умножить на один и тот же коэффициент q;

+ последовательность b_n, в которой каждый последующий член можно найти, если предыдущий умножить на один и тот же коэффициент q;

- последовательность b_n, в которой каждый предыдущий член можно найти, если последующий умножить на коэффициент q в степени (n+1);

- последовательность b_n, в которой каждый последующий член можно найти, если предыдущий разделить на коэффициент q в степени (n+1).

2. Из предложенного ряда найти геометрическую последовательность:

- 1…3…5…7…9…11

- 1…4…6…9…11…14

+ 1…2…4…8…16…32

- 1…2…6…12…36…72

3. Из предложенного ряда найти геометрическую последовательность:

+ 2…6…18…54

- 3…8…13…18

- 42…38…34…30

- 2…4…8…24

4. Из предложенного ряда найти геометрическую последовательность:

- 3…6…18…21…63

+ 4…12…36…108…324

- 17…15…13…11…9

- 2…4…12…24…72

5. Формула геометрической прогрессии – это

- b_n =b_(n+1)∙q , где b_n – член геометрической последовательности, q – коэффициент, b_(n+1) – последующий член геометрической последовательности;

- b_(n+1)=b_n∙qⁿ , где b_n – член геометрической последовательности, q – коэффициент, b_(n+1) – последующий член геометрической последовательности;

- b_(n+1)=b_(n-1)∙q , где b_(n-1) – предыдущий член геометрической последовательности, q – коэффициент, b_(n+1) – последующий член геометрической последовательности;

+ b_(n+1)=b_n∙q , где b_n – член геометрической последовательности, q – коэффициент, b_(n+1) – последующий член геометрической последовательности.

6. Формула общего члена геометрической прогрессии – это

- b_n=b₁∙q∙(n+1), где b_n – член геометрической последовательности, q – коэффициент, b₁ – первый член геометрической последовательности, n – порядковый номер члена геометрической прогрессии;

+ b_n = b₁∙q^(n-1), где b_n – член геометрической последовательности, q – коэффициент, n – порядковый номер члена геометрической прогрессии, b₁ – первый член геометрической последовательности;

- b_n = b₁∙q⁽ⁿ⁺¹⁾, где b_n – член геометрической последовательности, q – коэффициент, b₁ – первый член геометрической последовательности, n – порядковый номер члена геометрической прогрессии;

- b_n =b_(n+1)∙q^(n-1) , где b_n – член геометрической последовательности, q – коэффициент, n – порядковый номер члена геометрической прогрессии, b_(n+1) – последующий член геометрической последовательности.

7. При определении общего члена геометрической прогрессии, чему не должен равняться коэффициент q:

- 1

+ 0

- -1

- ∞

8. Записать формулу геометрической прогрессии для третьего члена геометрической прогрессии, если коэффициент q равен 1,2, а первый член b₁ составляет 5:

- b₃= b₁∙q∙(3+1)=5∙1,2∙4;

- b₃= b₁∙q⁽³⁺¹⁾=5∙1,2⁴ ;

- b₃= b₁∙q∙(3-1)=5∙1,2∙2;

+ b₃= b₁∙q^(3-1)=5∙1,2²

9. Записать формулу геометрической прогрессии для шестого члена геометрической прогрессии, если коэффициент q равен 2, а первый член b₁ составляет 7:

- b₆= b₁∙q∙(6+1)=7∙2∙7;

- b₆= b₁∙q⁽⁶⁺¹⁾=7∙2⁷ ;

- b₆= b₁∙q∙(6-1)=7∙2∙5;

+ b₆= b₁∙q^(6-1)=7∙2⁵

тест 10. Найти третий член геометрической прогрессии, если коэффициент q равен 1,2, а первый член b₁ составляет 5:

– 10,4

+ 7,2

– 24

– 12

11. Найти первый член b₁ геометрической прогрессии, если коэффициент q равен 2, а пятый член b₅ составляет 48:

– 4

- 0,75

+ 3

– 6

12. Найти коэффициент q, если первый член b₁ геометрической прогрессии равен 5, а десятый член b₁₀ составляет 11,79:

– 0,21

+ 1,10

- 0,24

– 1,15

13. Найти одиннадцатый член геометрической прогрессии, если коэффициент q равен 1,8, а первый член b₁ составляет 4:

– 1418,25

+ 1428,19

– 475

– 950

14. Найти первый член b₁ геометрической прогрессии, если коэффициент q равен 3, а седьмой член b₇ составляет 729:

– 1,5

- 0,95

+ 1

– 1,1

15. Найти коэффициент q, если первый член b₁ геометрической прогрессии равен 2, а четвертый член b₄ составляет 2:

– 1,25

+ 1

- 0,75

– 1,15

16. Формула суммы членов S_n геометрической прогрессии, когда известен n – ый и первый члены геометрической прогрессии:

-  где b_(n+1) – последующий член геометрической последовательности, q – коэффициент, b₁ – первый член геометрической последовательности, n – порядковый номер члена геометрической прогрессии;

+ где b_n – член геометрической последовательности, q – коэффициент, n – порядковый номер члена геометрической прогрессии, b₁ – первый член геометрической последовательности;

- где b_n – член геометрической последовательности, q – коэффициент, b₁ – первый член геометрической последовательности, n – порядковый номер члена геометрической прогрессии;

- где b_n – член геометрической последовательности, q – коэффициент, n – порядковый номер члена геометрической прогрессии, b₁ – первый член геометрической последовательности.

17. Формула суммы членов S_n геометрической прогрессии, когда известен только первый член геометрической прогрессии:

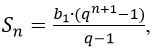- где q – коэффициент, b₁ – первый член геометрической последовательности, n – порядковый номер члена геометрической прогрессии;

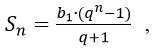- где n – порядковый номер члена геометрической прогрессии, b₁ – первый член геометрической последовательности;

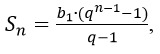- где b₁ – первый член геометрической последовательности, q – коэффициент, n – порядковый номер члена геометрической прогрессии;

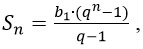+ где b_n – член геометрической последовательности, q – коэффициент, n – порядковый номер члена геометрической прогрессии.

18. При определении суммы геометрической прогрессии, чему не должен равняться коэффициент q:

+ 1

- 0

- -1

- ∞

19. Записать формулу суммы членов геометрической прогрессии, если порядковый номер члена геометрической прогрессии n равен 4, коэффициент q равен 3, а первый член b₁ составляет 1:

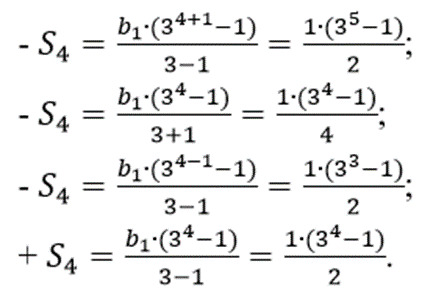
тест-20. Записать формулу суммы членов геометрической прогрессии, если третий член геометрической прогрессии равен 8, коэффициент q равен 2, а первый член b₁ составляет 2:

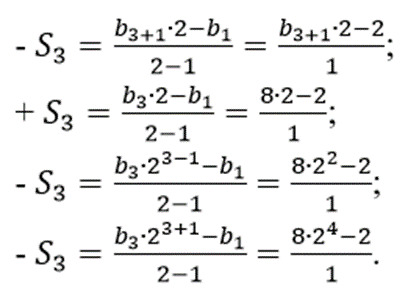
21. Найти сумму членов геометрической прогрессии, если порядковый номер члена геометрической прогрессии n равен 4, коэффициент q равен 3, а первый член b₁ составляет 1:

– 121

- 20

– 13

+ 40

22. Найти сумму членов геометрической прогрессии, если третий член геометрической прогрессии равен 8, коэффициент q равен 2, а первый член b₁ составляет 2:

– 80

+ 14

– 30

- 126

23. Найти сумму членов геометрической прогрессии, если порядковый номер члена геометрической прогрессии n равен 4, коэффициент q равен 3, а первый член b₁ составляет 1:

– 121

- 20

– 13

+ 40

24. Найти сумму членов геометрической прогрессии, если четвертый член геометрической прогрессии равен 192, коэффициент q равен 4, а первый член b₁ составляет 3:

– 75

+ 255

– 202

- 325

25. Найти сумму членов геометрической прогрессии, если порядковый номер члена геометрической прогрессии n равен 5, коэффициент q равен 1,25, а первый член b₁ составляет 2:

– 12,45

- 20,78

– 9,65

+ 16,41

26. Найти сумму членов геометрической прогрессии, если пятый член геометрической прогрессии равен 3,73, коэффициент q равен 1,2, а первый член b₁ составляет 1,8:

– 8,07

+ 13,39

– 30,47

- 12,3

27. Найти сумму членов геометрической прогрессии, если порядковый номер члена геометрической прогрессии n равен 3, коэффициент q равен 1,75, а первый член b₁ составляет 2,5:

– 12,18

- 18,72

– 13,45

+ 14,53

28. Найти сумму членов геометрической прогрессии, если шестой член геометрической прогрессии равен 1,61, коэффициент q равен 1,1, а первый член b₁ составляет 1:

– 7,77

+ 7,72

– 6,77

- 6,72

29. Характеристическое свойство для n - го члена геометрической последовательности b_n выражено формулой:

+ b_n² = b_n-1 · b_n+1 , где b_n – член геометрической последовательности, n – порядковый номер члена геометрической прогрессии, b_(n-1) – предыдущий член геометрической последовательности, b_(n+1) – последующий член геометрической последовательности;

- b_n = b_n-1 · b_n+1, где b_n – член геометрической последовательности, n – порядковый номер члена геометрической прогрессии, b_(n-1) – предыдущий член геометрической последовательности, b_(n+1) – последующий член геометрической последовательности;

- b_n² = b_n+1 ÷ b_n-1, где b_n – член геометрической последовательности, n – порядковый номер члена геометрической прогрессии, b_(n-1) – предыдущий член геометрической последовательности, b_(n+1) – последующий член геометрической последовательности;

- b_n = b²_n-1 · b²_n+1, где b_n – член геометрической последовательности, n – порядковый номер члена геометрической прогрессии, b_(n-1) – предыдущий член геометрической последовательности, b_(n+1) – последующий член геометрической последовательности.

тест_30. Каким цветом на рисунке отражен график геометрической прогрессии:

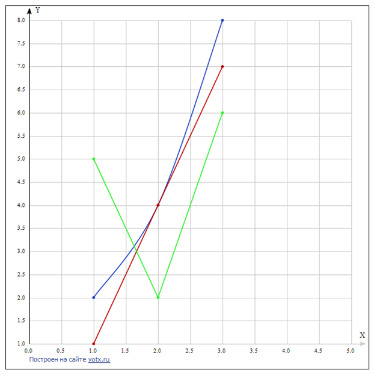
- геометрическая прогрессия не представлена на графике

- красный

+ синий

- зеленый