Тесты по алгебре 7 класс. Тема: "Введение в алгебру"
Правильный вариант ответа отмечен знаком +
1. При решении уравнений в первую очередь нужно:
+ раскрыть скобки, изменив выражение так, чтобы его смысл не изменился;
- привести подобные члены;
- выполнить все действия по порядку;
- перенести слагаемые с неизвестными множителями в левую часть.
2. Запись распределительного свойства сложения относительно умножения – это запись вида:
- ab + bc = ba + cb;
- a + b = b + a;
+ a (b + c) = ab + ac;
- abc = (ab)c.
3. Чтобы раскрыть скобки в выражении (a + b): c, нужно воспользоваться:
- распределительным свойством сложения относительно умножения;
+ распределительным свойством сложения относительно деления;
- переместительным свойством сложения;
- сочетательным свойством.
4. После приведения подобных слагаемых выражение x + 3x – 5x будет иметь вид:
+ -x;
- x;
- 3x;
- -2x.
5. После раскрытия скобок выражение -5 (x + 2) будет иметь вид:
- -5 + x + 2;
- -5x + 2;
- -5x + 10;
+ -5x – 10.
6. Какое выражение со скобками тождественно равно алгебраической сумме 2y3 – 8y:
- 2 (y3 – 8y);
- -2y (y2 – 4);
+ -2y (-y2 + 4);
- 2y (y2 + 4).
7. Раскрыв скобки в выражении -2,3 (-5x + 2y – 7), мы получим:
- -7,3x – 0,3y – 9,3;
+ 11,5x – 4,6y + 16,1;
- 2,7x + 4,3y – 4,7;
- -11,5x + 4,6y – 16,1.
8. Если привести подобные слагаемые в алгебраической сумме 5x + 13x – 18x, то результатом будет:
- произведение;
- сумма;
- число 1;
+ число 0.
9. Решением уравнения 2x + 7 = 4x – 3 будет:
+ х = 5;
- х = 2;
- х = -2;
- х = 12/3.
тест 10. Какое выражение можно составить для вычисления периметра фигуры, изображенной на рисунке:
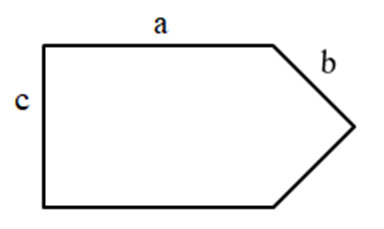


- a + b + c;
+ 2a + 2b + c;
- 2a + 2b + 2c;
- 2a + b + c.
11. Чтобы упростить выражение (3а – х) + (а + 2х), нужно:
- привести подобные;
+ раскрыть скобки и привести подобные;
- раскрыть скобки;
- ничего не нужно делать.
12. Сумма трех последовательных натуральных чисел, первое из которых равно m, представляет собой запись вида:
- m + 3;
- 3m;
- 3m + 1;
+ 3m + 3.
13. Для вычисления площади фигуры, изображенной на рисунке, будет составлено выражение:
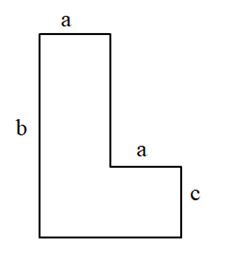
- a2 + bc;
- 2a + b + c;
+ ac + ab;
- a2bc.
14. Упростить выражение -2xy∙3yz, значит, привести его к виду:
+ -6xy2z;
- 6xyz;
- 5xyyz;
- -12xyz.
15. После сокращения дроби (-2xy)/4yz получится выражение:
- 2y/z;
+ -x/2z;
- (-x)/(-2z);
- (-2x)/z.
16. Для изготовления тонкой свечи необходимо m г воска, для свечи средней толщины нужно взять в 3 раза больше воска, а для самой толстой свечи – на 50г больше, чем для средней. Сколько грамм воска понадобится для изготовления трех разных свечей?
- (3m + 50) г;
- (4m + 50) г;
- (3m – 150) г;
+ (7m + 50) г.
17. Результатом упрощения выражения (x – y + z) – (x + y - z) будет:
- -2y;
- 2x;
+ -2y + 2z;
- 0.
18. Если привести подобные в алгебраической сумме 2a – 3b + a – 5a + 4b, получится выражение:
+ -2a + b;
- 8a – 7b;
- 3a + b – 5a;
- 3b – 4a.
19. Первое число равно x, второе число на 3 больше. Утроенная сумма этих чисел равна:
- 6x + 6;
- 12x;
+ 6x + 9;
- 5x + 9.
тест-20. Площадь квадрата S1 = a2, а площадь прямоугольника – S2 = ab. Чему будет равен периметр фигуры, образовавшейся при совмещении этих фигур?
- 2a + 2b;
- 6a + 2b;
- 5a + b;
+ 4a + 2b.
21. Чтобы получить алгебраическую сумму 2x – z, нужно упростить выражение:
- (x + y – z) – (2x + 2y + z);
+ (x – 2y + z) – (-x – 2y + 2z);
- (3x + y – 3z) – (x – y + 4z);
- (x – 2z) – (-x + z).
22. Периметр какой фигуры можно записать в виде выражения a + b + 2c?

23. Мама купила Вите футболку, шорты и кроссовки. Футболка стоит х руб., шорты на 50 руб. дешевле футболки, а кроссовки в 3 раза дороже, чем шорты. Какова стоимость покупки? Для решения задачи можно составить выражение:
+ 5x – 200;
- 5x + 200;
- 5x – 50;
- 5x + 50.
24. Участок земли поделили на 3 разных части: под картофель выделили х га, для огорода взяли 3/5 части картофельного надела, а площадь сада равна трем площадям огорода. Какова площадь всего участка?
- 4 3/5 x
+ 3 4/5 x
- 1 1/5 x
- 1 4/5 x
25. х = 1 – это корень уравнения:
- -2 (x + 2) = 3 (-x + 1);
- 2 (x – 2) = 3 (x – 1);
- 2 (x – 2) = 3 (x + 1);
+ -2 (x + 2) = 3 (-x – 1).
26. Выберите вариант, где выражения тождественно равны:
- (x + y) + (2x – y) и (x – y) – (4x –y);
- (x – y) – 2 (x + y) и (2x – 2y) + (-3x – y);
+ 2 (x + y) – (x – y) и (2x – y) – (x – 3y);
- 3y – 5x + 2x + y и 2y + x – 5y – 4x.
27. Фигура на рисунке состоит их трех разных квадратов. Какое выражение не подходит для вычисления площади этой фигуры?
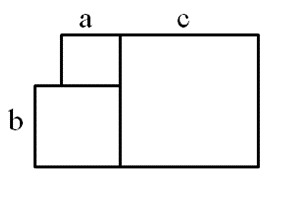
- a2 + b2 + c2;
+ b (c + a) + ac + c2
- c (a + c) + b (b – a);
- c2 + b (a + b) – a (b – a).
